In the complex numbers, where i = √(-1), the conjugate of any value a + bi is a– bi.What is the result when you multiply 2 + 7i by its conjugate?
-
Solution
The conjugate of 2 + 7i is 2 – 7i, so you’re looking for the value of (2 + 7i)(2 – 7i).
Begin by FOILing to remove the parentheses:
(2 + 7i)(2 – 7i) = 4 – 14i + 14i – 49i2 = 4 – 49i2
Now, because i = √(-1), you can substitute –1 for i2:
4 – 49(–1) = 4 + 49 = 53
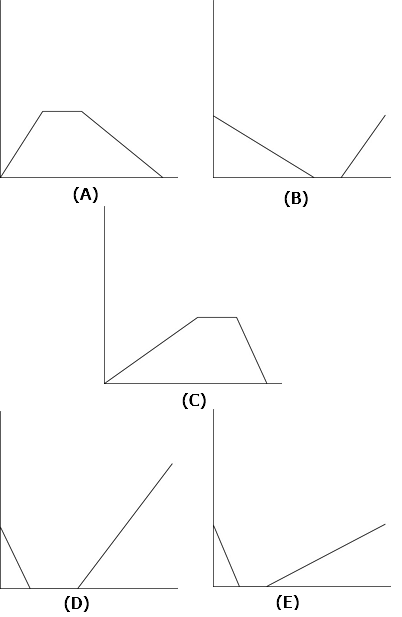
Jacob works as a lifeguard at a local pool. At the beginning of a 12-hour overnight shift, the pool was full, and Jacob began draining it. After 2 hours, the pool was completely empty. He spent 3 hours cleaning the pool and then began filling it up again. The pool finished filling just as his shift ended. Which of the following graphs accurately describes the amount of water in the pool throughout Jacob’s shift?
-
Solution
The water level decreases and then rises again, which rules out Choices (A) and (C).
The pool is full to capacity at the beginning of the shift, so it can’t have more water at the end of the shift; therefore, Choice (D) is also wrong.
Finally, the pool drains in 2 hours but takes 7 hours to fill, so the downward slope at the beginning of the shift is greater than the upward slope at the end; as a result, you can rule out Choice (B), leaving Choice (E) as the correct answer.
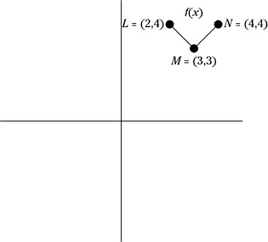
The following figure shows f(x), which includes points L,M,and n plus the line segments \(\overline{LM}\) and \(\overline{MN}\). Which of the following functions is equivalent to f(x)?
-
Solution
The function f(x) is symmetrical, so if you reflect it horizontally across the y-axis and then shift it 6 units to right, it returns to where it started.
To reflect it horizontally, change x to –x:
f(–x)
Now, to move this function 6 units to the right, change x in this new function to x – 6 and simplify:
f(–(x – 6)) = f(–x + 6) = f(6 – x)
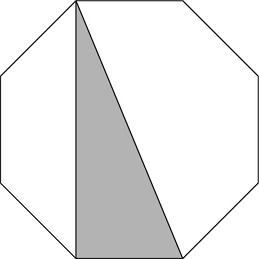
In the following figure, the regular octagon has a side with a length of 1. What is the area of the shaded region?
-
Solution
The octagon is regular, so the shaded region is a right triangle.
It has a base of 1, so you need to know its height to find its area.
Draw a few lines as follows to help find the height of the triangle:

If you let x equal the unknown length, the height of the shaded region is 2x + 1.
To find the value of x,notice that the length x is the leg of a 45-45-90 triangle with a hypotenuse of 1.
The ratio of a leg of this triangle to its hypotenuse is 1 : √2
Thus:
\(\frac{1}{\sqrt{2}} = \frac{x}{1}\)
Therefore:
\(x = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}\)
So
2x + 1 = √2 + 1
Plug this value as the height into the formula for the area of a triangle, with a base of 1:
\(A = \frac{1}{2}bh = \frac{1}{2}\left ( 1 \right )\left ( \sqrt{2} + 1 \right ) = \frac{\sqrt{2} + 1}{2}\)
To this questions below, use the following graph, which provides information about the number of new clients five salespeople registered last month.
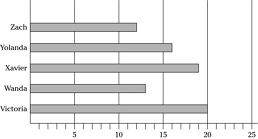
Suppose that next month Victoria registers twice as many clients as she did this month and that each of the other four salespeople registers the same number of clients as he or she did this month. In this case, what percentage of clients will Victoria have registered?
-
Solution
If Victoria doubles her registration to 40 and the others keep the same numbers, the sum of registrations will be:
12 + 16 + 19 + 13 + 40 = 100
Thus, Victoria’s registration will be:
40⁄100 = 40%
To this questions below, use the following graph, which provides information about the number of new clients five salespeople registered last month.

What percentage of the new clients did Yolanda register?
-
Solution
Zach registered 12 clients, Yolanda registered 16, Xavier registered 19, Wanda registered 13, and Victoria registered 20.
Add these together to find the total number of clients registered:
12 + 16 + 19 + 13 + 20 = 80
So Yolanda registered:
16⁄80 = 1⁄5 = 20%
Paulette, Quentin, and Rosie each donated money to a charity. Paulette gave as much money as Quentin and Rosie gave together. If Quentin had given three times more than he gave, he would have given $40 more than Paulette. And if Rosie had given $20 less, she would have given half as much as Paulette. How much did Paulette give?
-
Solution
Let p, q, and r equal the amounts that Paulette, Quentin, and Rosie gave, respectively.
Then you can set up the following three equations:
p = q + r ; 3q = p + 40 ; 2(r – 20) = p
Simplify the third equation
p = q + r ; 3q = p + 40 ; 2r – 40 = p
Substitute q + r for p into the second and third equations:
3q = q + r + 40 ; 2r – 40 = q + r
Simplify both equations:
2q = r + 40; r – 40 = q
Now substitute r – 40 for q into the equation 2q = r + 40 and solve for r:
2(r – 40) = r + 40
2r – 80 = r + 40
r – 80 = 40
r = 120
Substitute 120 for r in the equation 2r – 40 = p and solve for p:
2(120) – 40 = p
240 – 40 = p
200 = p
The following figure shows a cylindrical tank whose diameter is 3 times the length of its height. The tank holds approximately 231.5 cubic meters of fluid. Which of the following answer choices most closely approximates the height of the tank?
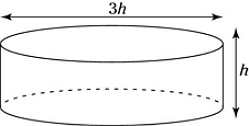
-
Solution
The height of the tank is hand its diameter is 3h, so its radius is 1.5h.
The volume of the tank is approximately 231.5 cubic meters.
Use 3.14 as an approximation of π and plug these values into the formula for a cylinder:
V = πr2h
231.5 = (3.14)(1.5h)2h
Simplify and solve for h:
231.5 ≈ (3.14)(2.25h2)h
231.5 ≈ 7.065h3
32.767 ≈ h3
3.2 ≈ h
Thus, the height of the tank is closest to 3 meters.
Which of the following is equal to sin x sec x?
-
Solution
First, use the reciprocal identity \(sec x = \frac{1}{cos x}\) to substitute for sec x:
\(sin x sec x = \frac{sin x}{cos x}\)
Now recall the following identity:
\(\frac{sin x}{cos x} = tan x\)
On the xy-plane, what is the area of a circle with this equation: (x + 3)2 + (y – 4)2 = 49?
-
Solution
The formula for a circle of radius r is (x – h)2 + (y – k)2 = r2.
So in the equation (x + 3)2 + (y – 4)2 = 49:
r2 = 49
r = 7
You now plug this value into the formula for the area of a circle to get your answer:
A = πr2 = π(7)2 = 49 π
