After polling a class of 24 students by a show of hands, you find that 9 students play soccer and 21 students play basketball. Given that information, what is the number of students in the class who must play both soccer and basketball?

F. zero
G. 1
H. 3
J. 6
K. 9

Solution

You are given that the total number of students is 24.

If 21 students play basketball, and 9 students play soccer, there must be some overlap between basketball players and soccer players.

The total number of students who play basketball and/or soccer is 21 + 9, or 30; therefore, 30 – 24, or 6 students must play both sports.

Which of the following describes the total number of dots in the first n rows of the triangular arrangement below?

A. 30
B. 2n
C. n²
D. n(n + 1)
E. 2n + 2(n − 1)

Solution

One approach to solving this problem is to make a table like the one below, showing the number of rows and the cumulative number of dots.

The total number of dots in rows 1 and 2 is 2(2+1);

the total number of dots in row 3 is 3(3+1), and so on.

You should be able to see that for the nth row, the total is the product of n and n + 1, or n(n + 1).

Using the complex number i, where i² = −1,\(\frac{2}{(1 − i)}\times \frac{(1 + i)}{(1 + i)}\)=?

F. 1 + i
G. i − 1
H. 1 − i
J. 2(1 + i)
K. 2(1 − i)

Solution

To find an equivalent expression for\(\frac{2}{(1 − i)}\times \frac{(1 + i)}{(1 + i)}\), simply perform the calculations, as follows:

\(\frac{2(1 + i)}{(1 − i)(1 + i)}=\frac{2(1 + i)}{(1 − i^{2})}\)

\(\frac{2(1 + i)}{(1 − i^{2})}=\frac{2(1 + i)}{2}\)

\(\frac{2(1 + i)}{2}= 1 + i\)

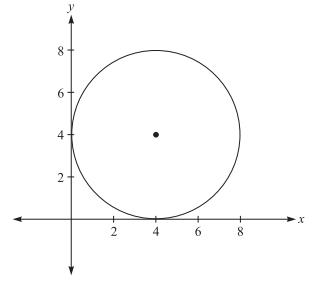
A circle in the standard (x, y) coordinate plane is tangent to the x-axis at 4 and tangent to the y-axis at 4. Which of the following is an equation of the circle?

A. x² + y² = 4
B. x² + y² = 16
C. (x − 4)² + (y − 4)² = 4
D. (x − 4)² + (y − 4)² = 16
E. (x + 4)² + (y + 4)² = 16

Solution

The best approach to this question is to draw a diagram as shown below:

The equation of a circle is (x−h)²+(y−k)² = r².

One way to find an equation for a circle is by using the coordinates of the center, (h, k), and the radius, r.

For this circle, the center is at (4, 4) and the radius is 4. Given center (4, 4) and radius 4, the circle has equation (x − 4)² + (y − 4)² = 42, or (x − 4)² + (y − 4)² = 16.

If you selected answer choice B, a common incorrect answer, you centered the circle at (0, 0).

The ratio of the radii of two circles is 9:16. What is the ratio of their circumferences?

F. 3:4
G. 9:16
H. 18:32
J. 3:4π
K. 9π:16

Solution

To find the ratio of the circumference of 2 circles for which the ratio of their radii is 9:16, recognize that both circumference and radius are 1-dimensional attributes of a circle.

Because of that, the ratios should be the same, 9:16. Another way is to use the ratio of the radii and let 9x and 16x be the radii of the two circles.

Their circumferences would be 2π(9x) and 2π(16x), respectively.

When you put them in a ratio you see that the ratio 2π(9x):2π(16x) simplifies to 9:16.

What is the distance in the standard (x, y) coordinate plane between the points (2,3) and (5,5)?

A. 3
B. 5
C. \(\sqrt{11}\)
D. \(\sqrt{13}\)
E. \(\sqrt{25}\)

Solution

To find the distance between 2 points in the standard (x, y) coordinate plane, use the distance formula, which states that d = \(\sqrt{[(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}]}\). Therefore, the distance is \(\sqrt{[(5-2)^{2}+(5-3)^{2}]}\), or (32 + 22),which equals \(\sqrt{13}\).

Another way to look at this problem would be to draw a picture as shown above. Then you can use the Pythagorean Theorem to find the hypotenuse of the triangle that is formed from the given points.

Let x ◙ y = (x − 2y)² for all integers x and y. Which of the following is the value of 5 ◙ (−3)?

A. 121
B. 64
C. 41
D. 1
E. −31

Solution

You are given that x ◙ y = (x−2y)² and are asked to solve 5 ◙ (−3). To do this,simply replace x with 5, and y with −3, as follows:
x ◙ y = (x − 2y)²
5 ◙ (−3) = (5 − 2(−3))²
5 ◙ (−3) = (5 − (−6))²
5 ◙ (−3) = (5 + 6)²
5 ◙ (−3) = (11)²
5 ◙ (−3) = 121

If 125% of a number is 425, what is 65% of the number?

F. 221
G. 276
H. 284
J. 308
K. 340

Solution

Because 125% of “the number” is 425,

then “the number” is 425 ÷ 1.25, which equals 340.

Calculate 65% of 340: 340 × 0.65 = 221.

Of the 517 graduating seniors at Brighton High School, approximately ⁴⁄₅ will be attending college, and approximately ¹⁄₂ of those going to college will be attending a state college. Which of the following is the closest estimate of the number of graduating seniors who will be attending a state college?

F. 170
G. 200
H. 260
J. 300
K. 320

Solution

To find out how many of the 517 seniors in Brighton High School are going to a state college, first find how many are going to college.

You are given that ⁴⁄₅ of the total number of graduating seniors (517) will be attending college: ⁴⁄₅ of 517 = 413.6, which can be rounded up to 414.

Now, calculate the number of those 414 seniors who are going to a state college:(¹⁄₂)(414), or about 207 seniors are going to a state college. This is closest to 200, answer choice G.

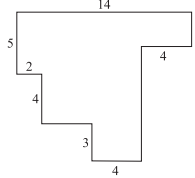
In the figure shown below, each pair of intersecting line segments meets at a right angle, and all the lengths are given in inches. What is the perimeter, in inches, of the figure?

A. 30
B. 36
C. 42
D. 52
E. 62

Solution

This figure has 10 sides, but the lengths are given for only 7 sides.

Those lengths add up to 36 inches.

The perimeter is greater than this because of the missing 3 sides so you can eliminate answer choices A and B.

To solve this problem, use the information given to find the missing sides; based on the figure, you can see that the sum of right-facing sides equals the sum of left-facing sides, and the sum of top-facing sides equals the sum of bottom-facing sides.

It is easy to see that the bottom-facing sides will equal the top-facing side, which has a length of 14.

Since we have the values for all of the left-facing sides (5 + 4 + 3 = 12), the right-facing sides also have the sum of 12.

Thus the perimeter is 14 + 14 + 12 + 12, or 52.

Attempted

0

Correct

0

Wrong

0

Complete