What is cos \(\frac{\pi }{12}\) given that \(\frac{\pi }{12}\) = π⁄3 − π⁄4 and that cos(α − β) = (cos α)(cos β) + (sin α)(sin β)?

-
Solution

If x = 3r − 4 and y = 3r + 2, which of the following expresses y in terms of x?
-
Solution
To obtain an expression for y in terms of x when x = 3r −4 and y = 3r +2,
first solve x = 3r − 4 for r as follows:
x = 3r − 4
x + 4 = 3r
\(\frac{x + 4}{3}=r\)Substitute that expression for r into y = 3r+2, and solve for y: y = 3\(\left [ \frac{x + 4}{3} \right ]\)+ 2, which simplifies to y = (x + 4) + 2, or y = x + 6.
A triangle, ΔABD, is reflected across the y-axis to have the image ΔA’B’D’ in the standard (x, y) coordinate plane: thus A reflects to A’ . The coordinates of point A are (m, n). What are the coordinates of point A’ ?
-
Solution
To find the coordinates of vertex A after it is reflected across the y-axis,remember that a reflection across the y-axis does not change the sign of the y-coordinate but does change the sign of the x-coordinate. Therefore, you can eliminate answer choices G, H, and J. You might sketch a figure like the one below.

The reflection of A (m, n) across the x-axis is A'(−m, n). The most popular incorrect answer is J, which gives the reflection of A over the line y = x.
Which of the following is the graph, in the standard (x, y) coordinate plane, of y = \(\frac{x^{2}+3x}{x}\)?
-
Solution
The equation y = \(\frac{x^{2} + 3x}{x}\) can be simplified to y = \(\frac{x(x + 3)}{x}\). Therefore, the graph of this seemingly complicated equation actually looks like a line, not a parabola, so eliminate answer choices A and B. This is equivalent to y = x + 3 except when x = 0. When x = 0, the original equation is undefined. So the correct graph is y = x + 3, with a point removed where x = 0.
If f (x) = 2x2 + 3, then f (x + h) = ?
-
Solution
To find f(x + h) when f(x) = 2x2 + 3, substitute (x + h) for x in f(x) = 2x2 + 3, as follows:
f (x + h) = 2(x + h)2 + 3
2(x + h)2 = 2(x2 + 2xh + h2) + 3
2(x2 + 2xh + h2) = 2x2 + 4xh + 2h2 + 3
Which of the following systems of inequalities is represented by the shaded region of the graph below?
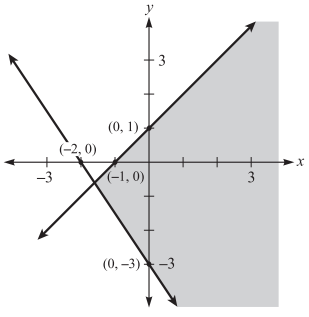
-
Solution
To find the system of inequalities represented by the shaded region of the graph, first find the equations of the line through (−1, 0) and (0, 1) and the line through (−2, 0) and (0, −3).
These are y = x + 1 (the y-intercept is 1) and y = (−3⁄2)x − 3 (the y-intercept is −3), respectively.
Pay attention to the coordinating conjunctions, and/or.
If sin θ = 4⁄5 and π⁄2 < θ < π, then tan θ = ?
-
Solution



John wants to draw a circle graph showing his friends’ favorite ice cream flavors. When he polled his friends asking each their favorite flavor of ice cream, 35% of his friends said chocolate, 20% of his friends said vanilla, 15% of his friends said strawberry, 25% of his friends said mint chocolate chip, and 5% of his friends said flavors other than those previously listed. What will be the degree measure of the vanilla sector of the circle graph?
-
Solution
You are given that 20% of John’s friends selected vanilla ice cream as their favorite flavor.
This means that 20% of the 360° in the circle will represent vanilla; 20% of 360 is equivalent to (0.20)(360°), or 72°.
If you chose one of the other answers, you may have found the degree measure of any of the other flavors.
Pentagons have 5 diagonals, as illustrated below. How many diagonals does the heptagon (7 sides) below have?
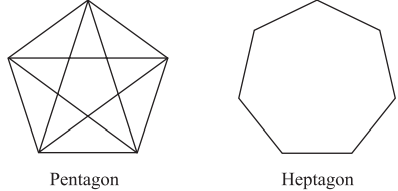
-
Solution
As shown below, there are 4 diagonals coming from each vertex point.

Because there are 7 vertex points, you might be tempted to conclude that there are 7×4, or 28 diagonals.
But this method counts each diagonal exactly twice.
Therefore, there are 28⁄2 , or 14 diagonals.
Which of the following is the set of all real numbers x such that x + 2 > x + 5 ?
-
Solution
To find the real numbers x such that x + 2 > x + 5, subtract x and 2 from both sides.
The result is 0 > 3, and because that inequality is never true, there is no solution for x.
The solution set is the empty set.





