If \(\frac{n^{x}}{n^{y}}\)= n2 for all n ≠ 0, which of the following must be true?
-
Solution
To solve this problem, recall that \(\frac{n^{x}}{n^{y}}\) = nx−y.
Since it is given in the problem that \(\frac{n^{x}}{n^{y}}\) = n2, you can conclude that nx−y = n2 and thus x − y = 2.
A triangle has sides of length 4.7 meters and 9 meters. Which of the following CANNOT be the length of the third side, in meters?
-
Solution
The key to solving this problem is remembering that the triangle inequality states that no one side of a triangle can be greater than the sum of the other two sides.
Thus the third side of the triangle in the problem cannot be greater than the sum of the other two sides, 4.7 and 9, which is 13.7.
Of the answer choices, only 14 is too large to be a possible value for the third side of the triangle.
In the standard (x, y) coordinate plane, what is the length of the line segment that has endpoints (−3,4) and (5,−6)?
-
Solution
To find the distance between two points (x1, y1) and (x2, y2), you can use the distance formula, which is d =\(\sqrt{(x_{2} − x_{1})^{2} + (y_{2} − y_{1})^{2}}\). The length of the line segment that has endpoints (−3,4) and (5,−6) will equal the distance between points (−3,4) and

What is the center of the circle with equation (x −3)2 + (y + 3)2 = 4 in the standard (x, y) coordinate plane?
-
Solution
To solve this problem, you need to know that the equation of a circle with center (h,k) and radius r is (x−h)2 +(y−k)2 = r2.
Therefore, the center of the circle in the problem,
(x − 3)2 + (y + 3)2 = 4, is (3,−3).
Which of the following is the solution set of x+2>−4?
-
Solution
To find the solution set of x+2>−4, first solve for x by subtracting 2 from both sides.
The result is x > −6. Thus the solution set is {x : x > −6).
In the standard (x, y) coordinate plane, what is the slope of the line joining the points (3,7) and (4,−8)?
-
Solution
To find the slope of the line between any two points (x1, y1) and (x2, y2), you can use the equation \(\frac{(y_{2} − y_{1})}{(x_{2} − x_{1})}\).
Therefore, when you have the points (3,7) and (4,−8) it follows that the slope of the line joining these points is \(\frac{(−8 − 7)}{(4 − 3)}=\frac{-15}{1}\) , or −15.
A rectangular parking lot that is 3 feet longer than it is wide has an area of 550 square feet. How many feet long is the parking lot?
-
Solution
If a rectangular parking lot has a length, l, that is 3 feet longer than its width, w, then l = 3+w, or w = l −3.
The area of a rectangle is equal to its length times it width, or A = lw. Since the area of this parking lot is 550, lw = 550. Substituting (l − 3) for
550 = l(l − 3) =
550 = l2 − 3l
l2 − 3l − 550 = 0.
To solve for l, factor the quadratic equation to get (l + 22)(l − 25) = 0, making l = −22 or l = 25.Since negative values for length do not make sense in this context, the length is 25.
All sides of a rhombus are the same length, as shown below.
If one diagonal is 12 inches long and the other is 32 inches long, how many inches long, to the nearest hundredth of an inch, is a side of the rhombus?
-
Solution
The diagonals of a rhombus intersect at their midpoints and form right angles as shown below.

Since the diagonals meet at their midpoints and form right angles, they form a right triangle with legs 12⁄2 = 6 and 32⁄2= 16. To find the length of a side of the rhombus, you can simply use the Pythagorean Theorem and solve where the side of the rhombus, s, is the hypotenuse: s2 = 62 + 162 = 292; s is approximately equal to 17.09.
For a certain quadratic equation, ax2 + bx + c = 0, the 2 solutions are x = 3⁄4 and x = −2⁄5. Which of the following could be factors of ax2 + bx + c?
-
Solution
For a certain quadratic equation ax2 + bx + c = 0, if x = a⁄b is a solution, then a possible factor would be (bx −a).
Since two solutions for ax2 + bx + c = 0 are x = 3⁄4 and x = −2⁄5, then possible factors are (4x − 3) and (5x + 2).
The area of a parallelogram may be found by multiplying the base by the height. What is the area, in square inches,of the parallelogram below?
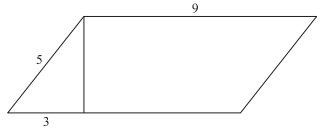
-
Solution
The height, h, can be found using the Pythagorean Theorem (c2 = a2 + b2):
52 = 32 + h2
25 = 9 + h2
h2 = 16, or h = 4.
Thus, when you multiply the base of the parallelogram by its height, the area of the parallelogram is 9 × 4 = 36.

