If you graph the lines 3x + 2y = –2 and 5x – y = 14 on a standard xy-graph, at which point will the lines intersect?
-
Solution
Solve the two equations, 3x+ 2y= –2 and 5x– y= 14, as a system of equations.
To do this, multiply the second equation by 2 and then add it to the first equation:
\(\frac{\begin{matrix} & 3x & + & 2y & = & -2\\ + & 10x & - & 2y & = & 28 \end{matrix}}{\begin{matrix} & 13x & \;\; & & \;\;\; = & 26 \end{matrix}}\)
Now solve for x:
x = 2
Replace x with 2 in either equation and solve for y:
3(2) + 2y = –2
6 + 2y = –2
2y = –8
y = –4
At the point of intersection, x = 2 and y = –4, so this point is (2, –4).
A rectangular box has two sides whose lengths are 3 centimeters and 9 centimeters and a volume of 135 cm3. What is the area of its largest side?
-
Solution
The box has dimensions of 3 and 9 and a volume of 135, so plug these values into the formula for the volume of a box:
V = lwh
135 = (3)(9)h
135 = 27h
5 = h
So the remaining dimension of the box is 5.
The two longest dimensions are 5 and 9, so the area of the largest side is 5 × 9 = 45.
If a and b are the two values of t that satisfy the equation t2 – 6t + 8 = 0, with a > b,what is the value of a – b?
-
Solution
Factor the left side of the equation:
t2 – 6t + 8 = 0
(t – 2)(t – 4) = 0
Split this equation into two equations and solve:
t – 2 = 0 or t – 4 = 0
t = 2 ; t = 4
Thus, a = 4 and b = 2.
So a – b = 4 – 2 = 2.
In the following figure, the two horizontal lines are parallel. Which of the following does NOT equal 180°?
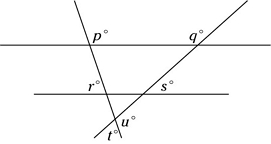
-
Solution
∠p and ∠r are opposite angles on the parallel lines, so they total 180°, which rules out Choice (A).
The same is true of ∠q and ∠s,ruling out Choice (C).
∠t and ∠u are supplementary, so they add up to 180°, which rules out Choice (E).
Finally, ∠r, ∠s, and ∠t are all vertical angles with the three interior angles of a triangle, so they total 180°, ruling out Choice (D).
By elimination, the correct answer is Choice (B).
If you multiply two integers together and then add 4, the result is 40. Which of the following could NOT be the sum of the two numbers?
-
Solution
Let the two integers equal x and y,and then create the following equation and simplify:
xy + 4 = 40
xy = 36
So x and y are a pair of integers that equal 36.
Try adding all possible combinations of two integers that multiply out to 36:
1 × 36 = 36; 1 + 36 = 37
2 × 18 = 36; 2 + 18 = 20
3 × 12 = 36; 3 + 12 = 15
4 × 9 = 36; 4 + 9 = 13
6 × 6 = 36; 6 + 6 = 12This list of sums includes 12, 13, 15, and 20, but not 18.
Thus, no pair of integers both satisfies the original equation and adds up to 18.
If f(x) = 4x2 – 5x – 5 and g(x) = 2x – 4, what is the value of \(\frac{g\left ( 6 \right )}{f\left ( -5 \right )}\)?
-
Solution
The problem states that f(x) = 4x2 – 5x – 5, so
f(–5) = 4(–5)2 – 5(–5) – 5 = 100 + 25 – 5 = 120
You also know that g(x) = 2x – 4, so
g(6) = 26 – 4 = 64 – 4 = 60
Therefore: \(\frac{g\left ( 6 \right )}{f\left ( -5 \right )} = \frac{60}{120} = \frac{1}{2}\)
If pq – 3r = 2, what is the value of q in terms of p and r?
-
Solution
Solve the equation pq – 3r = 2 in terms of p and r by isolating the q on one side of the equal sign as follows:
pq - 3r = 2
pq = 2 + 3r
\(q = \frac{3r + 2}{p}\)
In the following triangle, what is the value of sec n?

-
Solution
The secant of an angle equals the hypotenuse over the adjacent angle, so
sec n = \(\frac{H}{A} = \frac{2\sqrt{5}}{4} = \frac{\sqrt{5}}{2}\)
Andrea wants to fill in two sections of her backyard with sod that must be purchased in 2-x-2-foot squares. If the two sections measure 30 x 40 feet and 60 x 80 feet, how many squares of sod does she need to buy?
-
Solution
To begin, find the area of each of the two sections by multiplying the lengths of the sides:
30 feet ×40 feet = 1,200 square feet
60 feet ×80 feet = 4,800 square feet
The total area that needs sod has an area of 1,200 + 4,800 = 6,000 square feet.
Each individual square is 2 feet by 2 feet, so each has an area of 4 square feet.
Because all the numbers are even, there will be no waste when the squares of sod are placed.
Therefore, you just have to find the number of squares needed by dividing:
6,000 ÷ 4 = 1,500
What is the slope of a line on a standard xy-plane that passes through the point (1, 3) and (4, –3)?
-
Solution
Plug the values for the coordinates into the formula for the slope of a line:
Slope = \(\frac{y_{2} - y_{1}}{x_{2} - x_{1}} = \frac{-3 -3 }{4 - 1} = \frac{-6}{3} = -2\)