A square pool with an area of 81 square feet is to be placed entirely within a circular enclosure with a radius of 10 feet. Tiles will be laid within the entire enclosure around the pool (but not under it). What is the approximate area, in square feet, of the enclosure that will be tiled?
-
Solution
Since the area of the square pool is given, you must find the area of the circle, with a radius of 10, and subtract the area of the pool. The area of a circle is equal to πr2, where r is the radius. The area of this circle is 102π = 100π ≈ 314 square feet. Thus the area of the enclosure is approximately 314 − 81 = 233 square feet.
If 0◦ ≤ x ≤ 90◦ and tan x = 15⁄8 , then cos x = ?
-
Solution
Given that 0◦ ≤ x ≤ 90◦ and that tan x = \(\frac{15}{8}\) , x can be pictured in the right triangle below.

Because tangent is the ratio of the side opposite the angle to the side adjacent to the angle, the legs of the right triangle can be labeled as above. Cosine is the ratio of the side adjacent to the angle to the hypotenuse, which is not given. It is possible to eliminate answer choices in such a manner that it is not necessary to use the Pythagorean Theorem. Since the side adjacent to x is 8, the numerator in cos x will be 8, eliminating all but answers A and E. Since the legs of the triangle are 8 and 15, the hypotenuse will be longer than either, eliminating answer choice E. Thus cos x = \(\frac{8}{17}\).
What value of x will satisfy the equation 0.2(x − 2,700) = x?
-
Solution
To solve the equation 0.2(x − 2,700) = x, first distribute:
0.2x − 540 = x
− 540 = 0.8x
− 675 = x
The points R (2,2) and S (6,3) in the standard (x,y) coordinate plane below are 2 vertices of triangle RST, which has a right angle at S. Which of the following could be the third vertex, T?
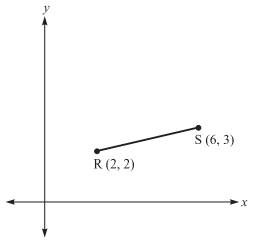
-
Solution
Because there is a right angle at S, the point T will lie along the line through S that is perpendicular to the segment RS. To solve this problem, find the equation for the line through S that is perpendicular to the segment RS and try each answer choice to find one that lies on the line. Since the line is perpendicular to segment RS, it will have a slope that is the opposite reciprocal of the slope of RS. Since slope is rise/run, the slope of RS is \(\frac{(3 − 2)}{(6 − 2)}=\frac{1}{4}\) . The slope of a line perpendicular to that is −4. Because a point and the slope of the line are known, the point-slope form of the equation can be utilized. A line through point (h, −k) with slope m has equation y − k = m(x − h). Thus the line through S (6,−3) that is perpendicular to the segment RS has equation y − 3 = −4(x − 6). Distributing and adding like terms, the result is y = −4x + 27. Of the answer choices, only the point (5,7) falls on the line.
The bowling league selects its 4 officers by first selecting the president, then the vice president, then the secretary, then the treasurer. If there are 40 bowlers who are eligible to hold office and no member can hold more than one office, which of the following gives the number of different possible results of the election?
-
Solution
To solve this problem, you would multiply the number of possibilities in each officer position. Since the league selects its 4 officers by first selecting the president, then the vice president, then the secretary, then the treasurer, there are 40 possibilities for president, 39 possibilities for vice president, 38 possibilities for secretary, and 37 possibilities for treasurer. The total number of different possibilities for the election is therefore 40 × 39 × 38 × 37.
In order to clean her aquarium, Stephanie must remove half of the water. The aquarium measures 30 inches long, 16 inches wide, and 12 inches deep. The aquarium is currently completely full. What volume of water, in cubic inches, must Stephanie remove?
-
Solution
To solve this problem, calculate the volume of the aquarium and divide by 2. Since volume is equivalent to length × width x height, the volume is 30 × 16 × 12, or 5,760 cubic inches of water. Dividing by two, you see that half of the tank would be 2,880 cubic inches of water.
One route along flat terrain from Hermansville to Melville is to drive straight north from Hermansville for 120 miles to Jamestown, then, at Jamestown, to drive straight west for 80 miles to Melville. If a straight, flat road existed between Hermansville and Melville, approximately how many miles long would it be?
-
Solution
The easiest way to solve this problem is to draw a picture similar to the one below.

Since the route heads straight north from Hermansville for 120 miles to Jamestown, and then straight west for 80 miles to Melville, the turn at Jamestown creates a right angle. If a straight, flat road existed between Hermansville and Melville, it would form the hypotenuse of a right triangle with legs 80 and 120. Using the Pythagorean Theorem (c2 = a2 + b2), you can see that the distance of this straight route from Hermansville to Melville would be:

(1⁄2)2 + (1⁄3)2 + (1⁄4)2 = ?
-
Solution

There are 16 ounces in one pound. If 3.4 pounds of beef cost $4.95, what is the cost per ounce, to the nearest cent?
-
Solution
To find the cost per ounce, first convert 3.4 pounds to ounces. Because there are 16 ounces in a pound, 3.4 pounds is 3.4(16) = 54.4 ounces. To find cost per ounce, divide the cost in dollars by the number of ounces, or \(\frac{\$ 4.95}{54.4}\) ounces = $0.09 per ounce.
In the standard (x, y) coordinate plane, what is the y-intercept of the line given by the equation 3x + 5y = 8?
-
Solution





