If 8a⁶b³ < 0, then which of the following CANNOT be true?

F. b < 0
G. b > 0
H. a = b
J. a < 0
K. a > 0

Solution

In order for 8a⁶b³ to be less than zero, either 8 or a⁶ or b³ must be less than zero. However, it is obvious that 8 > 0 and any number taken to an even power is non negative. Thus b³<0 and in order for that to be true, b<0. Of the answer choices, only b>0 CANNOT be true.

In the parallelogram below, lengths are given in inches. What is the area of the parallelogram, in square inches?

A. √94
B. 7√47
C. 49
D. 63
E. 16√47

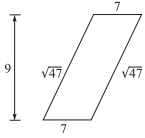
Solution

The area of a parallelogram is equal to base × height. In the figure, you can see that the base of the parallelogram is 7 and the height of the parallelogram is 9. Thus, the area of the parallelogram is 9 × 7 = 63.

The volume of a cube is given by the formula s³, where s is the length of a side. If a cube has a volume of 64,and the length of each side is halved, the new cube’s volume will be:

F. 3
G. 6
H. 8
J. 16
K. 32

Solution

In order to solve this problem, you must realize that since the volume of a cube is equal to the cube of its sides, multiplying the length of the sides by ¹⁄₂ will have the effect of multiplying the volume by (¹⁄₂)³= ¹⁄₈. The cube in this problem has a volume of 64, so if you halve the length of each side, new cube’s volume will be 64(¹⁄₈)= 8.

For the area of a square to triple, the new side lengths must be the length of the old sides multiplied by:

A. √3
B. 3
C. 4
D. 2√3
E. 9

Solution

Since the area of a square is equal to the square of its sides, multiplying the sides by √3 will have the effect of multiplying the area by (√3)² = 3.

When measured from a point on the ground that is a certain distance from the base of a cell phone tower, the angle of elevation to the top of the tower is 41°, as shown below. The height of the cell phone tower is 200 feet. What is the distance, in feet, to the cell phone tower?

F. 200 tan 41°
G. 200 sin 41°
H. 200 cos 41°
J. 200 sec 41°
K. 200 cot 41°

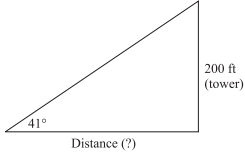
Solution

What is the solution set of |3a − 2| ≤ 7?

A. {a: a ≤ 3}
B. {a: −⁵⁄₃ ≤ a ≤ 3}
C. {a: −⁵⁄₃ ≥ a ≥ 3}
D. {a: −⁵⁄₃ ≤ a ≥ 3}
E. {a: −⁵⁄₃ ≥ a ≤ 3}

Solution

To find the solution set for |3a − 2| ≤ 7, break it up into two separate inequalities: 3a − 2 ≤ 7 and 3a − 2 ≥ −7. Starting with 3a − 2 ≤ 7, solving for a yields a ≤ 3. With 3a − 2 ≥ −7, solving for a yields a ≥ −⁵⁄₃.Thus a is between −⁵⁄₃ and 3 inclusive.

The value of b that will make ^b⁄₃ +2 = ¹⁄₄ a true statement lies between which of the following numbers?

F. −4 and −6
G. −1 and −3
H. −1 and 1
J. 1 and 3
K. 3 and 5

Solution

To simplify calculations, you can multiply the entire equation by 12 to obtain whole numbers and get 4b + 24 = 3.

Subtracting 24 from both sides yields 4b = −21.

Dividing by 4 yields b = −\(\frac{21}{4}\) , which is a little less than −5.

Thus the correct answer will lie between −4 and −6.

Which of the following operations will produce the smallest result when substituted for the blank in the expression:²⁄₃ ____ − 3?

A. plus
B. minus
C. multiplied by
D. divided by

Solution

In the figure below, tan ϕ = ?

F.¹⁄_√2
G. √2
H. 1
J. 3
K. 3√2

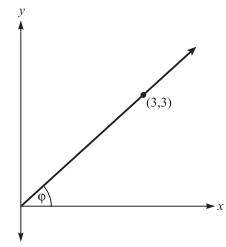
Solution

Tangent is the ratio of the side opposite to the side adjacent to an angle in a right triangle. Drawing a line that passes through (3,3) and is perpendicular to the x-axis creates a right triangle, as shown in the figure (see below).

Because point (3,3) is given, both legs of the right triangle have a length of 3. Thus tan ϕ = ³⁄₃ = 1.

In the standard (x,y) coordinate plane, which of the following lines goes through (3,4) and is parallel to y = 2x + 2?

A. y = ¹⁄₂x + 2
B. y = 2x − 2
C. y = 2x + 4
D. y = 2x + 10
E. y = 3x + 2

Solution

Remember that all parallel lines have the same slope, so a line parallel to y = 2x + 2 will a slope of 2. A quick way to aid you in solving this problem would be to eliminate answer choices that do not have slope 2, so answer choices A and E can be immediately eliminated. Check the point (3,−4) in the remaining answer choices. The only choice that works is y = 2x − 2.

Attempted

0

Correct

0

Wrong

0

Complete