Points A, B, and C are three distinct points that lie on the same line. If the length of AB is 19 meters and the length of BC is 13 meters, then what are all the possible lengths, in meters, for AC?

F. 6 only
G. 32 only
H. 6 and 32 only
J. Any number less than 32 or greater that 6
K. Any number greater than 32 or less than 6

Solution

Since AB is longer than BC, there are only two possible configurations: B is between A and C or C is between A and B. In the case that B is between A and C, AC = AB + BC = 19 + 13 = 32. In the case that C is between A and B, AC = AB − BC = 19 − 13 = 6. Therefore, AC can be 6 and 32 only

The first and second terms of a geometric sequence are a and ab, in that order. What is the 643rd term of the sequence?

A. (ab)⁶⁴²
B. (ab)⁶⁴³
C. a⁶⁴²b
D. a⁶⁴³b
E. ab⁶⁴²

Solution

Refer to the following chart to follow the patter of the sequence.

Since the power of b is one less than the number of term, the nth term will be abⁿ⁻¹. The 643rd term will then be ab⁶⁴³⁻¹ = ab⁶⁴².

Given the vertices of parallelogram QRST in the stan dard (x, y) coordinate plane below, what is the area of triangle QRS, in square units?

F. 24
G. 28
H. 48
J. 60
K. 80

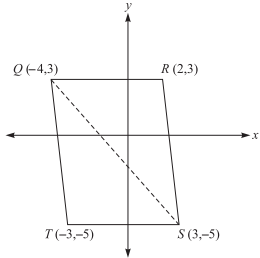
Solution

Remember that the area of a parallelogram is equal to base × height. In this case, the base is [3 − (−3)] or [2 − (−4)], both of which equal 6, and the height is (3 − (−5)) = 8. Thus the area is 6 × 8 = 48. The area of triangle QRS,[¹⁄₂(b)(h)], is half the area of the parallelogram, or 24.

Three distinct lines, all contained within a plane, separate that plane into distinct regions. What are all of the possible numbers of distinct regions of the plane that could be separated by any such three lines?

A. 4, 6, 7
B. 4, 5, 6
C. 3, 5, 7
D. 3, 5, 6
E. 3, 4, 5

Solution

Start by drawing 3 parallel lines.

Now, try drawing 3 lines in other configurations, and you will see that there will always be either 6 or 7 regions:

Therefore, the correct answer is 4, 6, or 7 distinct regions, answer choice A.

What is the smallest possible value for the product of 2 integers that differ by 7?

F. 8
G. 0
H. −6
J. −10
K. −12

Solution

The smallest possible value will occur when it is negative. A negative product will result only when one of the numbers is positive and one is negative. The possible pairs are then −1 and 6, −2 and 5, −3 and 4, −4 and 3, −5 and 2, and −6 and 1. Of these pairs, the smallest product is (−3)(4) = (−4)(3), or −12.

The measure of the vertex angle of an isosceles triangle is (a + 30)°. The base angles each measure (2a − 15)°. What is the measure in degrees of one of the base angles?

A. 36°
B. 45°
C. 57°
D. 66°
E. 90°

Solution

To solve this problem, you must remember that in an isosceles triangle, the base angles have the same measure.

Since the sum of angles is 180◦ for all triangles, 180 = (a + 30)+2(2a−15).

Distributing and adding like terms yields
180 = (a + 30) + 4a − 30
180 = 5a
a = 36
Since the base angles are equivalent to 2a − 15, they equal 2(36) − 15 = 72 − 15, or 57°.

In the standard (x,y) coordinate plane, what is the equation of the line that passes through the origin and the point (3,4)?

F. y = ¹⁄₄x + ³⁄₄
G. y = ¹⁄₄x - ¹⁄₃
H. y = ⁴⁄₃x
J. y = ¹⁄₂x + ³⁄₄
K. y = ⁹⁄₄x

Solution

To solve this problem, remember that the formula for slope is equal \(\frac{(y_{2} − y_{1})}{(x_{2} − x_{1})}\), where (x₁, y1) and (x2, y2) are two given points on a line.

The equation of the line that passes through the origin and the point (3,4) will have slope \(\frac{(4 − 0)}{(3 − 0)}=\frac{4}{3}\).

Since the line passes through the origin, the y-intercept is 0. Thus the correct equation is y = ⁴⁄₃x.

In a game, 80 marbles numbered 00 through 79 are placed in a box. A player draws 1 marble at random from the box. Without replacing the first marble, the player draws a second marble at random. If both marbles drawn have the same ones digit (that is, both marbles have a number ending in 0, 1, 2, 3, etc.), the player is a winner. If the first marble drawn is numbered 35, what is the probability that the player will be a winner on the next draw?

A.\(\frac{1}{79}\)
B.\(\frac{7}{80}\)
C.\(\frac{7}{79}\)
D.\(\frac{1}{10}\)
E.\(\frac{8}{79}\)

Solution

Of the 80 marbles, only 8 end in 5. If the first marble is drawn and not replaced, there are 79 marbles left, 7 of which have a ones digit of 5. Thus the probability that the player will be a winner is ⁷⁄₇₉.

If a system of 2 linear equations in 2 variables has NO solution, and 1 of the equations is graphed in the (x,y) coordinate plane below, which of the following could be the equation of the other line?

F. y = −2
G. y = −¹⁄₄x + 2
H. y = −2x − 4
J. y = ⁴⁄₃x + 2
K. y = 4x − 4

Solution

In order for a system of 2 linear equations to have no solutions, the graphs of the equations must be parallel. Parallel lines have the same slope. To find the equation whose graph is parallel to the line in the figure, you must find the slope of the line between the points (0,−4) and (3,−0). Since slope is \(\frac{rise}{run}\), the slope is ⁴⁄₃. The only equation with the correct slope of ⁴⁄₃ is y = ⁴⁄₃ x +2.

If log₄x = 3, then x = ?

A.\(\frac{1}{log_{12}}\)
B. 4 log³
C. 12
D. 64
E. 81

Solution

Logarithms are used to indicate exponents of certain numbers called bases. By definition, log_ab = c, if a^c= b. If log₄ x = 3, then x = 4³, or 64.

Attempted

0

Correct

0

Wrong

0

Complete