In the figure below, ABCD is a trapezoid. Point E lies on line AD, and angle measures are as marked. What is the measure of angle BDC?
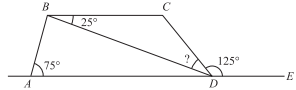
-
Solution
To find the measure of ∠BDC in the figure, it is helpful to recognize that the sides BC and AD are parallel (definition of trapezoid) and are connected by the transversal BD. ∠CBD and ∠ADB are alternate interior angles, and thus are equal and both measure 25°. Because A, D, and E all lie along the same line, ∠ADE = 180°. Because ∠ADE is made up of ∠ADB, ∠BDC, and ∠CDE, you know that the measures of these three angles add up to 180°. If x is the unknown angle measure, then 25° + x + 125° = 180°; thus x is equal to 30°.
The average of 7 consecutive numbers is 16. What is the sum of the least and greatest of the 7 integers?
-
Solution
You can apply common sense to solve this problem. If the average of 7 consecutive integers is 16, it would make sense that the middle number is 16 (this assumption only holds because there are an odd number of integers and because the integers are consecutive). Thus, the list of consecutive integers is 13, 14, 15, 16, 17, 18, 19. The sum of the first and last integers is 13 + 19 = 32.
A circle is circumscribed within a square with sides of 12 feet, as shown below. What is the area of the circle, to the nearest square foot?
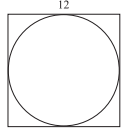
-
Solution
Recall that the area of a circle with radius r is πr2. The radius of the circle can be found by taking half of the distance across the circle, which in this case is also equal to half of the length of the side of the square. Thus the area of the square is π62 = about 113 square feet. If you selected answer choice A you found the area of the square.
When x is divided by 7, the remainder is 4. What is the remainder when 2x is divided by 7?
-
Solution
You are given that x divided by 7 leaves a remainder of 4. The easiest approach to this problem is to assume that 7 goes into x one time, with a remainder of 4. Therefore, x is equal to 11. If x = 11, then 2x = 22. When 22 is divided by 7, the remainder is 1.
The product of two integers is between 137 and 149. Which of the following CANNOT be one of the integers?
-
Solution
For the product of two integers to lie between 137 and 149, a multiple of both integers must lie between 137 and 149. Of the answer choices, 15 is the only number without a multiple that lies between 137 and 149; 15 × 9 = 135, and 15 × 10 = 150. Thus, the only number that cannot be one of the integers is 15.
In the (x, y) coordinate plane, what is the y-intercept of the line −9x − 3y = 15?
-
Solution
To find the y-intercept of the line −9x − 3y = 15, convert the equation to slope-intercept form. To so do, first add 9x to both sides to get −3y = 9x + 15. Then divide by −3 to get y = −3x − 5. Since the slope-intercept form of the equation is y = −3x − 5, the slope is −3 and the y-intercept is −5.
In the figure below, \(\overline{XY}\) = \(\overline{YZ}\). If a = 40◦, than \(\overline{XY}\) =?
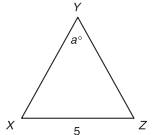
-
Solution
To solve this problem, first recognize that, since \(\overline{XY}\) = \(\overline{YZ}\), the triangle is isosceles. Because the triangle is isosceles, you know that angles X and Z are congruent and have equal measure. If a = 40°, then 180° = 40° + x° + y° and x° + y° = 140°. Since x = y, both angles equal 70◦. In triangles, sides have lengths that are proportional to their opposite angles. Because you know that the length of \(\overline{XZ}\) is 5, and \(\overline{XZ}\) is opposite the 40° angle, you can set up a proportion to find the length of side \(\overline{XY}\) using its opposite angle, 70°, as follows:
5/40 = \(\overline{XY}\)/70
5 = 40(\(\overline{XY}\)/70)
(5 × 70) = 40\(\overline{XY}\)
= 350/40 = 8.75
In the figure below, the perimeter of the triangle is 12+4√3 inches. What is the value of x, in inches?
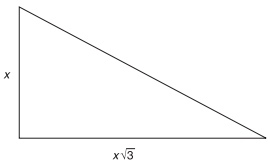
-
Solution
To solve this problem, recognize that the triangle is a “special triangle.” A right triangle in which the length of the longer leg is √3 times the length of the shorter leg is a 30◦−60◦−90◦ right triangle. Another property of this type of right triangle is that the hypotenuse is 2 times the length of the shorter leg. So, this right triangle has lengths x, x √3, and 2x. The perimeter is the sum of the lengths of the sides. You are given that the perimeter equals 12 + 4 √3. Set the two equations equal and solve for x:
12 + 4√3 = x + x√3 + 2x
12 + 4√3 = 3x + x√3For the right side of the equation to equal the left side of the equation, x must be equal to 4.
For all pairs of real numbers M and N where M = 6N + 5, N = ?
-
Solution
To solve the equation M = 6T + 5 for N you could subtract 5 from both sides to get M − 5 = 6N, and then divide by 6 on both sides to get \(\frac{(M − 5)}{6}\).
Points B and C lie on segment AD as shown below. Segment AD is 32 units long, segment AC is 23 units long, and segment BD is 27 units long. How many units long, if it can be determined, is segment BC?
![]()
-
Solution
To find the length BC when the length AD is 32 units, the length AC is 23 units, and the length BD is 27 units, and the points are along the segment AD as shown in the problem, you must notice that segment BC is the intersection of segment AC and the segment BD. So, the sum of the lengths AC and BD is the same as the sum of the lengths AD and BC. Using the actual lengths, solve for BC as follows:
AC + BD = AD + BC
23 + 27 = 32 + BC
50 = 32 + BC
18 = BC