How many different positive three-digit integers can be formed if the three digits 3, 4, and 5 must be used in each of the integers?
-
Solution
To solve, write out every possible three-digit integer: 345, 354, 435, 453, 534, and 543; six different positive three-digit numbers can be formed, answer choice F.
What is the value of log4 64?
-
Solution
Logarithms are used to indicate exponents of certain numbers called bases. By definition, loga b = c, if ac = b. To solve, let log4 64 = x; therefore, 64 = 4x. Because 43 = 64, x = 3.
For real numbers r and s, when is the equation |r −s| = |r + s| true?
-
Solution
To solve this problem, it might be helpful to use test values for r and s and systematically try the scenario presented in each answer choice. The equation |r − s|=|r + s| is true only when r = 0 or s = 0.
In the pentagon, shown below, one interior angle measures 40◦. What is the total measure of the other 4 interior angles?
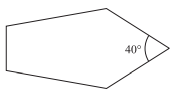
-
Solution
The sum of the interior angles of a pentagon is (5 − 2)(180◦), or 540◦. Thus, the total of the other 4 angles is 540◦ − 40◦, or 500◦.
The sides of a triangle are 9, 12, and 15 centimeters long. What is the angle between the 2 shortest sides?
-
Solution
A triangle with sides 9, 12, and 15 centimeters long has sides in the ratio of 9:12:15, which simplifies to 3:4:5. Recall that a 3 − 4 − 5 triangle is a special case because it is known to be a right triangle. Any triangle with sides in the same ratio is also a right triangle. Thus, there is a right angle between the smaller sides.
What is the distance in the standard (x,y) coordinate plane between the points (0,1) and (4,4)?
-
Solution
To find the distance between 2 points in the standard (x, y) coordinate plane you can use the distance formula d =\(\sqrt{[(x_{2} − x_{1})^{2} + (y_{2} − y_{1})^{2}]}\). Calculate the distance as follows:
\(\sqrt{[(4 − 1)^{2} + (4 − 0)^{2}]}=\sqrt{(3^{2}+4^{2})}=\sqrt{25}=5\)
What is the smallest possible integer for which 15% of that integer is greater than 2.3?
-
Solution
To solve this problem, make x the smallest possible integer for which 15% of x is greater than 2.3. Then, set up the following inequality: 0.15x > 2.3. Divide both sides by 0.15 to get x > 15.333, repeating. The smallest integer greater than the repeating decimal 15.333 is 16.
If x and y are positive integers such that the greatest common factor of x2y2 and xy3 is 27, then which of the following could y equal?
-
Solution
You could take a “bruteforce” approach and test all the given values of y and see if you could find an x that worked. For example, if y = 9, then the two numbers are x2×92 and x × 93. You can see that 92 is a factor of these 2 numbers, so 27 cannot be the greatest common factor.
It might be more efficient to be more general and avoid testing all 5 values of x. Notice that xy2 is a common factor of both x2y2 and xy3. Because it is a factor, xy2 must also be a factor of 27. Well, 27 factors as 3 × 32, so it seems natural to see if x = 3 and y = 3 are possible solutions. In this case the two numbers from the problem are 32 × 32 and 33 × 3 and the greatest common factor is 3 × 32 = 27, so it works.
For what value of n would the following system of equations have an infinite number of solutions?
3a + b = 12
12a + 4b = 3n
-
Solution
Systems of equations have an infinite number of solutions when the equations are equivalent. In order for the two equations to be equivalent, the constants and coefficients must be proportional. If the entire equation 3a + b = 12 is multiplied by 4, the result is 4(3a + b) = 4(12), or 12a + 4b = 48. Thus in order for the two equations to be equivalent, 3n = 48, or n = 16.
For which of the following functions is f (−5) > f (5)?
-
Solution
To solve this problem, first eliminate answer choices that yield equal values for f (−5) and f (5). These include answer choices in which the functions have even powers of x such as answer choice A, where f (x) = 6x2, answer choice B, where f (x) = 6, and answer choice E, where f (x) = x6 + 6. Now, substitute −5 and 5 into the remaining answer choices:
Answer choice C: f (x) = 6/x. When x is −5, f (x) = −6/5, and when x is 5, f (x) = 6/5. Therefore, f (5) is greater than f (−5) and answer choice C is incorrect.
Answer choice D: f (x) = 6 − x3. When x = −5, f (x) = 6 − (−125) or 131, and when x is 5, f (x) = 6 − 125, or −116. Therefore, f (−5) is greater than f (5).