ACT
Practice Test 29
Previous Solution Next

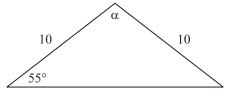
In the figure below, what is the measure of ∠α?

  • Solution

    The triangle pictured is isosceles, meaning that the two angles opposite the sides that have equal length have equal measure. Since the sum of the interior angles of a triangle is 180◦, the measure of ∠α is 180◦ − 2(55◦), or 180◦ − 110◦, which is 70◦.

If x = 3yz2, what is y in terms of x and z?

  • Solution

    To get y in terms of x and z, solve x = 3yz2 for y, as shown below:
    x = 3yz2
    \(\frac{x}{3z^{2}}=y,\: or\: y=\frac{x}{3z^{2}}\)

A rectangular garden has a length of x and a width of y. The garden has its length reduced by 3 feet and its width extended by 2 feet. What is the area of the new garden?

  • Solution

    You are given that a rectangular garden has a length of x and a width of y, and has its length reduced by 3 feet and its width extended by 2 feet. Therefore, the length becomes x − 3 and its width becomes y + 2. The area of the new garden is then (x − 3)(y + 2).

In the standard (x, y) coordinate plane, if the x-coordinate of each point on a line is 5 more than half the y-coordinate, what is the slope of the line?

  • Solution

    If the x-coordinate of each point on a line is 5 more than half the y-coordinate, then x = y 2 + 5. To find the slope of the line, solve for y and put the equation in slopeintercept form (y = mx + b, where m is the slope).
    To do so, first subtract 5 from both sides, then multiply the entire equation by 2 to get y = 2x−10. The slope is 2.

In the parallelogram PQRS shown below, PS is 7 centimeters long. If the parallelogram’s perimeter is 40 centimeters, how many centimeters long is PQ?

  • Solution

    The perimeter is the distance around the parallelogram. In parallelograms, opposing sides have equal lengths. If PS is 7 cm long, so is QR. Also, PQ and SR will have the same length. Set the length of PQ and SR to l, and solve.
    7 + 7 + l + l = 40
    14 + 2l = 40
    14 + 2l = 40
    l = \(\frac{26}{2}\) , or 13.

Which of the following is a value of r for which (r + 2)(r − 3) = 0?

  • Solution

    The expression (r + 2)(r − 3) will equal zero when either r + 2 or r − 3 equals zero. Thus r = −2 or r = 3.

Bus X travels 40 miles per hour for 2 hours; Bus Y travels 60 miles per hour for 11⁄2hours. What is the difference, in miles, between the number of miles traveled by Bus X and the number of miles traveled by Bus Y?

  • Solution

    To find the difference in the distance traveled, first find the distance traveled by each bus. Distance equals rate multiplied by time. Since Bus X travels 40 miles per hour for 2 hours, it traveled 40(2) = 80 miles. Likewise, since Bus Y travels 60 miles per hour for 11⁄2 hours, it traveled 60(1.5) = 90 miles. Therefore, the difference is 90 − 80, or 10 miles.

Contributions to the school dance fund are made by each of 4 student groups according to the table below.

What is the average dollar amount of the contributions made by the 4 student groups?

  • Solution

    To find the average, divide the sum of the contributions by the number of contributions, as follows:

    \(\frac{(25 + 40 + 30 + 15)}{4}=\frac{110}{4}= 27.50\)

To keep up with rising costs, a carpenter needs to increase his $30.00 per hour rate by 18%. What will be his new hourly rate?

  • Solution

    To calculate the new hourly rate, multiply the current rate by 18%, or 0.18, its decimal equivalent, and add the result to the current rate:
    30(0.18) + 30 = 30 + 5.40, or $35.40

One foot is equivalent to approximately 0.3048 meters.If a building is 65-feet long, what is the length of the building in meters, to the nearest tenth?

  • Solution

    You are given that one foot is approximately 0.3048 meters. Therefore, a building that is 65 feet long will be 65(0.3048), or 19.8 meters long.

Attempted

0

Correct

0

Wrong

0

Complete
Math Solved Practice Test
Attempted
Wrong
Correct