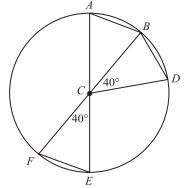
In the circle shown below, C is the center and lies on segments \(\overline{AE}\) and \(\overline{BF}\). Which of the following statements is NOT true?

F. ∠BAC measures 70◦
G. \(\overline{AB}\) is parallel to \(\overline{EF}\)
H. \(\overline{AB}\) ≅ \(\overline{BD}\)
J. ∠BCE ≅ ∠DCF
K. \(\overline{CF}\) ≅ \(\overline{EF}\)

Solution

The statement that CF is congruent to EF is not true because CEF is an isosceles triangle in which CE and CF are equal. Since the triangle is isosceles, ∠CFE is congruent to ∠CEF, and they have measure 70◦. In a triangle, the length of a side is proportional to the measure of the angle opposite it. Since the measure of the angle opposite EF is only 40◦ while the measure of the angle opposite CF is 70◦, EF must be shorter than CF.

What are the values for a that satisfy the equation (a + y)(a + z) = 0?

A. −y and −z
B. −y and z
C. −yz
D. y and −z
E. y and z

Solution

In order for the expression (a + y)(a + z) to equal zero, either a + y = 0 or a + z = 0. Thus either a = −y or a = −z.

\(\frac{−6}{\left | -3 \right |}=?\)

F. −3
G. −2
H. 0
J. 2
K. 9

Solution

The absolute value of any number is non-negative. Since | − 3| = 3, the value of \(\frac{--6}{\left | -3 \right |}=\frac{-6}{3}\), or −2.

A system of linear equations is shown below.
4y = 3x + 12
−4y = −3x − 8
Which of the following describes the graph of this system of linear equations in the standard (x, y) coordinate plane?

A. Two parallel lines with negative slope
B. Two parallel lines with positive slope
C. A single line with negative slope
D. A single line with positive slope
E. Two perpendicular lines

Solution

To see the properties of each linear equation more clearly, convert each to slope-intercept form (y = mx + b, where m is the slope and b is the y-intercept). The equation 4y = 3x + 12 becomes y = \(\frac{3x}{4}\) + 3 after you divide by 4. The equation −4y = −3x−8 becomes y = \(\frac{3x}{4}\) + 2 after you divide by −4. It is now clear that the equations are lines with slope ³⁄₄, making them parallel lines with positive slope. However,since they have different y-intercepts, they are two distinct lines.

If x² = 36 and y² = 81, which of the following CANNOT be the value of x + y?

F. −15
G. −3
H. 0
J. 3
K. 15

Solution

If x² = 36 and y² = 81, then x = ±6 and y = ±9. There are then 4 possible combinations of x + y: 6 + 9, −6 + 9, 6 + (−9), and −6 + (−9), which have values 15, 3, −3, and −15, respectively. Therefore, the value of x + y
cannot be 0.

A survey is conducted among 700 high-school students to see who their favorite college basketball teams are. If 250 students like the Hawks, 200 students like the Vikings, 50 students like the Bears, and the remaining students like the Warriors, approximately what percentage of the 700 high school students answered that the Warriors were their favorite team? (round to the nearest tenth of a percentage point)

A. 14.3%
B. 28.6%
C. 42.9%
D. 56.2%
E. 78.6%

Solution

Which of the following is a value of n that satisfies log_n64 = 2?

F. 4
G. 6
H. 8
J. 12
K. 32

Solution

Logarithms are used to indicate exponents of certain numbers called bases. By definition, log_ab = c, if a^c = b. Therefore, log_n 64 = 2 implies that 64 = n². Thus n = 8.

Reduce\(\frac{x^{8}y^{12}}{x^{4}y^{3}z^{2}}\)to its simplest terms.

A.\(\frac{x^{2}y^{12}}{z^{2}}\)
B.\(\frac{x^{2}y^{12}}{z^{2}}\)
C.x⁴y⁹z²
D. x²y¹²z²
E.\(\frac{x^{2}y^{9}}{z^{2}}\)

Solution

In the standard (x, y) coordinate plane, if a square has the vertices (−2,−3), (2,−3), and (2,1), what is the set of coordinates for the final vertex?

F. (2,−1)
G. (1,−2)
H. (−1,2)
J. (−2,−1)
K. (−2,1)

Solution

To solve this problem it might be helpful to draw a picture like the one below.

Since the figure is a square, the placement of the missing point becomes clear: the upper left corner. The point will share the same x-coordinate as (−2,−2) and the same y-coordinate as (2,1), making its coordinates (−2,1).

Which of the following is the product of (3x² − 1)(x² − 4)?

A. 3x⁴ + 13x² + 4
B. 3x⁴ + 5
C. 3x⁴ − 13x² + 4
D. 3x⁴ − 12x² + 4
E. 3x⁴ + 12x² + 4

Solution

To solve this problem, distribute using the FOIL method, as follows:
(3x² − 1)(x² − 4)
First: 3x⁴
Outside: −12x²
Inside: −x²
Last: 4
Combine like terms and simplify to get 3x⁴ − 13x² + 4.

Attempted

0

Correct

0

Wrong

0

Complete