A right triangle that has sides measured in the same unit of length is shown below. For any such triangle, (tan α)(sin β) is equivalent to:

-
Solution
To find the product (tan α)(sin β), break up tan α and sin β to their ratios. The ratio tan α is the side opposite α divided by the side adjacent to α:
z⁄x. The ratio sin β is the side opposite β divided by the hypotenuse: x⁄y. The product (tan α)(sin β) is, therefore,(z⁄x)(x⁄y)= z⁄y.
Three years ago, the population of a certain species of bird was calculated at 20 birds per acre. This year, a biologist recorded a total of 47 birds in an area equal to 3.25 acres. By about what percentage has the bird population in the biologist’s sample decreased over the last 3 years, to the nearest tenth?
-
Solution
This question asks you to calculate the percentage by which the population has decreased. First, determine the number of birds that you would expect to find in your sample area if the population density had not changed. Multiply the population density 3 years ago (20 birds) by the size of the sample area (3.25 acres):
20 × 3.25 = 65
You would expect to find 65 birds in your sample area if there had been no change in population density.
Next, subtract the actual number of birds recorded in the sample area (47) from the expected number of birds (65):
65 − 47 = 18
There are 18 fewer birds in the sample area than what you would expect to find. Since you are asked to calculate the percentage decrease, set up a proportion:
18 birds is to 65 birds as x percent is to 100 percent.
\(\frac{18}{65}=\frac{x}{100}\)
Cross-multiply and solve for x:
65x = 1,800
\(x=\frac{1,800}{65}\)
Since the problem asks for an answer to the nearest tenth, round to 27.7. According to the study, the population density of the particular bird that you are studying has decreased by approximately 27.7%.
Answer choice C could be obtained if you found the difference between the number of birds expected (65) and the number of birds recorded (47), then divided by the number of birds recorded (47) to get a percent. Answer choice D is the percentage that the number of birds per acre 3 years ago (20) is of the number of birds recorded in 3.5 acres this year (47).
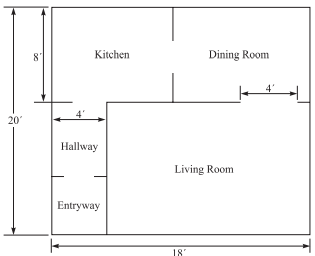
The figure above shows the plan for the ground floor of a townhouse. The thickness of the walls should be ignored when answering the questions. The dimensions shown are in feet, and each region is rectangular
What is the perimeter, in feet, of the ground floor of the townhouse?
-
Solution
The perimeter is equal to the distance around an object. To calculate the perimeter of the ground floor of the townhouse, add the sides. The perimeter of the ground floor of the townhouse is 2(20') + 2(18'), or 40'+ 36',which is 76'.
.

The figure above shows the plan for the ground floor of a townhouse. The thickness of the walls should be ignored when answering the questions. The dimensions shown are in feet, and each region is rectangular
What is the area, in square feet, of the living room?
-
Solution
To calculate the area of the living room, first calculate its dimensions. The length of the living room is 18' less the width of the hallway, which is 4', making it 18 − 4 = 14'. The width of the living room is 20' less the width of the kitchen, which is 8' , making it 20−8 = 12'. Thus the area of the living room is 14'×12'= 168 square feet.
Given that y − 5 = 1⁄2x + 1 is the equation of a line, at what point does the line cross the x axis?
-
Solution
A graph crosses the x-axis at the point when y = 0. Given that y − 5 = \(\frac{1}{2x}\) +1, let y = 0 such that −5 = \(\frac{1}{2x}\) +1. Subtracting 1 from both sides yields −6 = \(\frac{1}{2x}\). Multiplying by 2 yields −12 = x.
If the inequality |m| > |n| is true, then which of the following must be true?
-
Solution
One possible method of solving this problem is to systematically eliminate wrong answer choices. It is given that |m| > |n|.
Assuming that statement is true, then m cannot equal n because if m = n, then |m|=|n|; eliminate answer choice A. Pick numbers for the variables to more clearly see the relationships, as follows:
Answer choice B: When m = 3 and n = 2,|m| > |n| is true. Likewise, when m = −3 and n = −2, |m| > |n| is true. Therefore, answer choice B is correct.
Answer choice C: When m = 2 and n = 3, |m| > |n| is not true, so answer choice C is incorrect.
Answer choice D: When m = 3 and n = −4, |m| > |n| is not true, so answer choice D is incorrect.
Answer choice E: Because you are not given any information about n, you cannot determine a relationship, so answer choice E is incorrect.
If x + y = 13 and 2y = 16, what is the value of x?
-
Solution
To solve this problem, first solve the equation 2y = 16 for y to get y = 8. Then substitute y = 8 into the equation x + y = 13 to get x + 8 = 13, making x = 5.
What number can you add to the numerator and denominator of 5⁄8 to get 1⁄2?
-
Solution
To solve this problem, go through and try each answer choice to see which one has the desired result. The correct answer is −2 because adding negative 2 is the same as subtracting 2: \(\frac{(5 − 2)}{(8 − 2)}\)=
3⁄6, or 1⁄2.
Which of the following is the least common denominator for the expression below?
\(\frac{1}{a^{2} \times b \times c}+\frac{1}{b^{2}\times c}+\frac{1}{b \times c^{2}}\)-
Solution
The least common denominator (LCD) is actually the least common multiple of the three denominators. To find the LCD, first find the greatest common factor of the denominators. In this case, each denominator contains either a, b, or both b and c, so those are the factors that they have in common. The values that remain in the three denominators represent what they don’t have in common, and are the least common multiples of each denominator. To find the least common multiple, otherwise known as the least common denominator (LCD), simply multiply the least common multiples of each denominator together, to get a2 × b2 × c2.
What is the slope of the line given by the equation 21x − 3y + 18 = 0?
-
Solution
To find the slope, convert the equation 21x − 3y + 18 = 0 to slope-intercept form (y = mx+b, where m is the slope and b is the y-intercept). To do so, first subtract 18 and 21x from both sides to get −3y = −21x − 18. Then divide both sides by −3 to get y = 7x = 6. Therefore the slope is 7.