A rectangular kitchen is 8 feet longer than it is wide. Its area is 240 square feet. How long, in feet, is it?
-
Solution
A rectangular kitchen that is 8 feet longer than it is wide with width w would have length l = w + 8, or w = l − 8. Since the area A = 240 = lw, substitute w = l − 8 into 240 = lw to get 240 = l(l − 8) = l2 − 8l, or l2 −8l−240 = 0. To find l, factor l2−8l−240 = 0 into (l + 12)(l − 20) = 0. Thus l = −12 (which doesn’t make sense because a kitchen cannot have a negative length), or l = 20.
What is the equation of the circle in the standard (x, y) coordinate plane that has a radius of 4 units and the same center as the circle determined by x2 +y2 −6y+4 = 0?
-
Solution
A circle with center (h, k) and radius r has equation (x−h)2+(y−k)2 = r2. In order to determine the equation of the circle in the standard (x, y) coordinate plane that has a radius of 4 units and the same center as the circle determined by x2 + y2 − 6y + 4 = 0, first determine the center of the circle defined by x2 + y2 − 6y + 4 = 0 by converting the equation to the standard form for a circle (complete the square):
x2 + y2 − 6y + 4 = 0
x2 + y2 − 6y + 9 + 4 − 9 = 0
(no net change in value)
x2 + (y2 − 6y + 9) + 4 − 9 = 0 (regroup)
x2 + (y − 3)2 + −5 = 0 (factoring)
x2 + (y − 3)2 = 5
Thus the center of the circle is (0,3). A circle that has a radius of 4 units and the same center has the equation x2 + (y − 3)2 = 16.
The perimeter of a square is 36 units. How many units long is the diagonal of the square?
-
Solution
If the perimeter of a square is 36 units, then each side is 9 (since perimeter in a square is 4(s) where s is the length of a side). To find the length of the diagonal, you can use the Pythagorean Theorem because the diagonal is the hypotenuse of a right triangle with legs of length 9.
Thus d2 = 92 +92, or 81+81, which equals 2(81),
and d = \(\sqrt{(2(81))}\), or √2 \(\sqrt{81}\), which is 9√2.
If y ≠ z, what are the real values of x that make the following inequality true?
\(\frac{xy − xz}{3y − 3z}\) < 0
-
Solution


What is cos\(\frac{5\pi }{12}\) given that\(\frac{5\pi }{12}\) = π⁄4 + π⁄6 and that cos(α + β) = (cos α)(cos β) − (sin α)(sin β)? (Note: You may use the following table of values.)
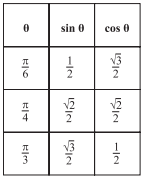
-
Solution

What is the solution set of |3a − 3| ≥ 12?
-
Solution
To solve this problem, remember that |3a − 3| ≥ 12 is equivalent to 3a − 3 ≥ 12 or 3a − 3 ≤ −12. Adding 3 to both sides and dividing by 3 yields a ≥ 5 or a ≤ −3.
Which of the following calculations will yield an even integer for any integer a?
-
Solution
Any integer when multiplied by an even integer results in an even integer. Also, the addition of any two even integers yields another even integer. Thus, regardless of the value of a or the power of a, multiplying by an even integer and adding an even integer will yield an even integer. This only occurs in the calculation 6a4 + 6.
For what value of b would the following system of equations have an infinite number of solutions?
3x + 5y = 27
12x + 20y = 3b
-
Solution
Systems of equations have an infinite number of solutions when the equations are equivalent (i.e. they graph the same lane). In order for the two equations to be equivalent, the constants and coefficients must be proportional. If the entire equation 3x + 5y = 27 is multiplied by 4, the result is 4(3x + 5y) = 4(27), or 12x + 20y = 108. Thus, in order for the two equations to be equivalent, 3b = 108, or b = 36.
If r and s are constants and x2 + rx + 12 is equivalent to (x + 3)(x + s), what is the value of r?
-
Solution
To solve this problem, multiply the expression (x + 3) by (x + s) to get x2 + 3x + sx + 3s. You are given that x2 + rx + 12 is equivalent to x2 + 3x + sx + 3s.
Therefore, 3s is equal to 12, making s equal to 4. It is also apparent that 3x + sx is equivalent to rx.
Set the quantities equal and solve for r, as follows:
rx = 3x + sx
rx = x(3 + s)
r = 3 + s
Because s = 4,r must equal 7.
A certain rectangle is 5 times as long as it is wide. Suppose the length and width are both tripled. The perimeter of the second rectangle is how many times as large as the perimeter of the first rectangle?
-
Solution
Regardless of the dimensions of a rectangle, tripling the length and width will always have the effect of tripling the perimeter because perimeter is directly proportional to length and width (P = 2l + 2w).


