37 is what percent of 144, to the nearest percent?
-
Solution
To find what percent 37 is of 144, divide 37 by 144 and multiply by 100%:
\(\frac{37}{144}\) ≈ 0.26
0.26 × 100% = 26%.
The sum of the real numbers a and b is 13. Their difference is 5. What is the value of ab?
-
Solution
If the sum of the real numbers a and b is 13, then a+b = 13. If the difference between a and b is 5, then |a−b| = 5. Think of the difference as the positive distance between a and b on the number line. Solve the first equation for a, as follows:
a + b = 13
a = 13 − b
Now, substitute 13−b for a in the second equation and solve for b:
|13 − b − b| = 5
|13 − 2b| = 5
| − 2b| = 8
| − b| = 4
b = 4
Now substitute b in the first equation to get a+4 = 13, so a = 9. If a = 9 and b = 4, ab = 36.
The isosceles triangle below has one angle measure as shown. What is the measure of each of the other angles?

-
Solution
Since the triangle is isosceles, the base angles will have the same measure, x.
Since the sum of the angles in a triangle is 180°, 50 + 2x = 180, making x =\(\frac{(180 − 50)}{2}\)= \(\frac{132}{2}\), or 65°
Which of the following numbers is the least in value?
-
Solution
Recall that in scientific notation 2.0 × 102 = 2.0 × 100 = 200 and 2.0 × 10−2 = 2.0 × 0.01 = 0.02. To solve this problem, determine the decimal value of each answer choice by changing the scientific notation to decimals:
A. 0.02 × 104 = 0.02 × 10,000 = 200
B. 0.2 × 103 = 0.2 × 1000 = 200
C. 2.0 × 10−2 = 2.0 × 0.01 = 0.02
D. 20.0 × 102 = 20.0 × 100 = 2000
E. 0.002 × 105 = 0.002 × 100,000 = 200
Thus 2.0 ×10−2 = 2.0×0.01 = 0.02 is the number that is least in value.
In the figure shown below, AD = 16, ED = 11, and AE is congruent to CD. What is the length of AB?\
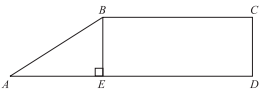
-
Solution
To solve this problem, first note that AB is the hypotenuse of a right triangle with legs AE and BE, then apply the Pythagorean Theorem. According to the figure, E is between A and D, which means that AD = AE + ED, or AE = AD − ED. It is given that AD = 16 and ED = 11, therefore AE = 16−11, or 5. Also according to the figure, you can reasonably assume that BE and CD have the same length, and since AE is congruent to CD, the segments BE and CD have a length of 5 as well. Thus, AB is the hypotenuse of a right triangle with legs of 5, making AB2 = 52 + 52 = 25 + 25, or 50. Since AB2 = 50, AB = \(\sqrt{50}\) = \(\sqrt{(50\times 2)}\) = \(\sqrt{25}\)√2, or 5√2.
4a3 × 5a8 = ?
-
Solution
To solve this problem, recall that when two numbers that consist of the same base and different exponents are multiplied together, you keep the base and add the exponents. Because multiplication is commutative, the expression 4a3 × 5a8 can be written as 4 × 5 × a8 × a3, or 20a8+3, which equals 20a11. You can eliminate answer choice A, B, and C because they add the coefficients instead of multiplying them.
What is the value of the expression 10(100x−10,000) + 100 when x = 250?
-
Solution
To solve this problem, substitute the value 250 for x in the expression 10(100x − 10, 000) + 100, as follows:
10(100(250) − 10,000) + 100 =
10(25,000 − 10,000) + 100 =
10(15,000) + 100 =
150,000 + 100 = 150,100.
2x2 × 3x2y2 × 5x2y is equivalent to:
-
Solution
To multiply these quantities, first group like terms:
2x2 × 3x2y2 × 5x2y = (2 × 3 × 5)(x2x2x2)(y2y).
To multiply the same base, add the exponents:
(2 × 3 × 5)(x2x2x2)(y2y) = 30x6y3.
All CDs are equally priced. If 8 CDs cost $76.00, what is the cost of 1 CD?
-
Solution
If all CDs are equally priced and 8 CDs cost $76.00, then the cost of 1 CD is \(\frac{\$ 76.00}{8}\), or $9.50.
Which of the following lists all the positive factors of 32?
-
Solution
The positive factors of 32 include all of the positive integers that divide evenly into 32. Don’t get confused between positive integers (which include 1) and even integers.