If 4(x − 2) + 5x = 3(x + 3) − 11, then x = ?
-
Solution
To solve this problem, first distribute and combine like terms before attempting any algebra:
4(x − 2) + 5x = 3(x + 3) − 11
4x − 8 + 5x = 3x + 9 − 11
9x − 8 = 3x − 2
6x = 6
x = 1
A clock tower casts a 150-foot shadow on level ground, as shown below. The angle of elevation from the tip of the shadow to the top of the tower is 40◦. To the nearest tenth of a foot, what is the height of the clock tower?
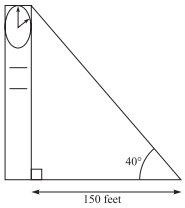
(Note: cos 40◦ = sin 50◦ ≈ 0.77
cos 50◦ = sin 40◦ ≈ 0.64
tan 50◦ ≈ 1.19
tan 40◦ ≈ 0.84)
-
Solution
To solve this problem, let the height of the clock tower be x. Using the fact that the figure shown forms a right triangle with legs 150 and x, the height of the clock tower can be calculated using the trigonometric ratio tangent. Because the tangent of an angle is the ratio of the side opposite an angle to the side adjacent to the angle, tan 40◦ = \(\frac{x}{150}\). In the problem it is given that tan 40◦ ≈ 0.84, making 0.84 = \(\frac{x}{150}\), or x = 150(0.84) = 126.0. The height of the clock tower is therefore 126.0 feet.
If f (x) = −3x2 − 8, then f (−4) = ?
-
Solution
To solve this problem, substitute −4 for x in the expression −3x2 − 8, as follows (remember to keep track of the negative signs!):
− 3(−4)2 − 8
= − 3(16) − 18
− 48 − 8 = −56
If you did not keep track of the negative signs, you would most likely arrive at one of the incorrect answer choices.
Which real number satisfies (2n)(8) = 163?
-
Solution
To solve this problem, recall that bxby = bx+y and (bx)y = bxy. Given (2n)(8) = 163, it will be helpful for this problem to think of 8 as 23 and 16 as 24. Thus (2n)(8) = (2n)(23) = 2n+3, and 163 = (24)3 = 212. Since(2n)(8) = 163, it follows that 2n+3 = 212 and that n + 3 = 12. Therefore n = 12 − 3 = 9.
On the real number line, what is the midpoint of −3 and 11?
-
Solution
To find the midpoint on a number line, take the average of the two points. The average of −3 and 11 is \(\frac{(−3 + 11)}{2}\) = 8⁄2, or 4, answer choice H. This is the same as applying the midpoint formula, which, given two points on a line, can be expressed as \(\left (\frac{[x_{1} + x_{2}]]}{2},\frac{[y_{1}+y_{2}]}{2}\right )\).
Rana and Tom own a pizza shop, which offers 3 kinds of cheese, 4 kinds of meat toppings, and 5 kinds of vegetable toppings. Each type of pizza on the menu has a combination of exactly 3 ingredients: 1 cheese, 1 meat, and 1 vegetable. How many types of pizzas are possible?
-
Solution
To solve this problem, multiply the number of possibilities for each option. Since there are 3 kinds of cheese, 4 kinds of meat toppings, and 5 kinds of vegetable toppings and each type of pizza on the menu has a combination of exactly 3 ingredients: 1 cheese, 1 meat, and 1 vegetable, the total number of pizza types that are possible is 3 × 4 × 5 = 60.
A certain brand of cereal costs $3.25 per box before sales tax is added. When you buy 5 or more boxes of this cereal you receive 1 additional box for free. What is the average cost per box of cereal for 6 boxes before sales tax is added?
-
Solution
To solve this problem, first find the cost of 5 boxes of cereal, then divide that total by 6. Since each box costs $3.25, the cost for 5 boxes is 5(3.25), or $16.25. Since each additional box is free, the average cost per box for the 6 boxes is \(\frac{\$ 16.25}{6}\) , or $2.71.
For all n, (3n + 5)2 = ?
-
Solution
To solve, use the FOIL (First, Outside, Inside, Last) method for binomial multiplication to expand (3n+5)2. It may be helpful to picture (3n + 5)2 as (3n + 5)(3n + 5). Using the FOIL method, (3n+5)(3n+5) becomes 9n2+15n+ 15n+25, which can be reduced to 9n2 +30n+25.
The Moondance Riding Academy held its annual horse show for 3 days. The total amount collected in entry fees for the 3 days was $1,450. The amount collected, in dollars, is shown for each of the 3 days in the bar graph below:
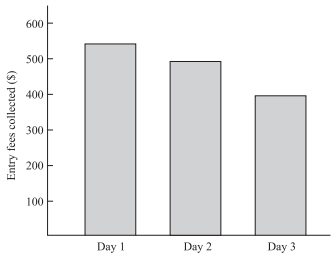
The mean amount collected per day during the 3-day period is what, to the nearest dollar?
-
Solution
To solve this problem, divide the total amount collected by the number of days:
\(\frac{1450}{3}\) = about $483 per day.
The Moondance Riding Academy held its annual horse show for 3 days. The total amount collected in entry fees for the 3 days was $1,450. The amount collected, in dollars, is shown for each of the 3 days in the bar graph below:

Approximately what percent of the money collected from entry fees over the 3 days was collected on Day 2?
-
Solution
To solve this problem, divide the amount collected on Day 2 (about $500 according to the graph) by the total collected, $1,450, and multiply by 100%:500
\(\frac{500}{1450}\times 100\)% ≈ 34%.