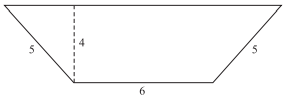
The area of a trapezoid is found by using the equation 1⁄2h(b1+b2), where h is the height and b1 and b2 are the lengths of the bases. What is the area of the trapezoid shown below?
-
Solution
To solve this problem, first determine the length of the top base using the Pythagorean theorem.
Since the height is 4 and the length of one of the diagonal sides is 3, the length of the other leg of the triangle is 3.
The top base equals the length of the bottom base plus twice the leg of the triangle just calculated.
Thus the length of the top base is 6+2(3) = 12.
Using the formula for the area of a trapezoid,1⁄2h(b1 + b2), A = 1⁄2(4)(6 + 12), or 36.
For right triangle ABC with dimensions in centimeters as given below, what is tan C?

-
Solution
Recall that the tangent of an angle in a right triangle is the ratio of the side opposite the angle to the side adjacent to the angle. From the figure shown of ABC, the side opposite angle C is 9 and the side adjacent to C is 5.
Therefore tan C = 9⁄5.
Which of the following statements is NOT true about the geometric sequence 36, 18, 9, …?
-
Solution
To solve this problem, systematically evaluate each answer choice for correctness.
From the sequence 36, 18, 9, ..., it is clear that each term is 1⁄2 of the preceding term; eliminate answer choice H. The fourth term is 9⁄2, or 4.5 and the fifth term is \(\frac{4.5}{2}\) , or 2.25, so eliminate answer choices F and G. While the first three terms are evenly divided by 3, the fourth and fifth (and any term following) are not evenly divisible by 3, so answer choice J is correct.
Which of the following equations expresses z in terms of x for all real numbers x, y, and z, such that x5 = y and y3 = z?
-
Solution
To solve this problem, substitute x5 = y for y in y3 = z. The equation y3 = z becomes (x5)3 = z, or z = x15, answer choice E.
In the standard (x, y) coordinate plane below, the points (0,2), (8,2), (3,6), and (11,6) are the vertices of a parallelogram. What is the area, in square units, of the parallelogram?

-
Solution
The area of a parallelogram is bh, where b is the length of the base and h is the height perpendicular to the bases. The length of the base can be determined by subtracting the x-coordinates of the points that determine the bases: 8 − 0 = 11 − 3 = 8 units long. The height, since it is the height perpendicular to the bases, can be determined by subtracting the y-coordinates of the points: 6 − 2 = 4. Therefore the area is bh = (8)(4), or 32.
(6a − 12) − (4a + 4) = ?
-
Solution
To solve this problem, combine like terms, keeping track of the negatives. The expression (6a −12)−(4a +4) becomes 6a − 12 − 4a − 4, which can be simplified to 2a − 16. The coefficient 2 can be factored out of both terms to get 2(a − 8)
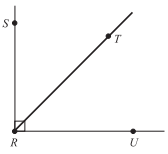
In the figure shown below, the measure of ∠ SRT is (x +15)° and the measure of ∠ SRU is 90°. What is the measure of ∠ TRU?
-
Solution
According to the figure, it is clear that ∠SRT and ∠TRU are complementary (they add up to 90°).
Therefore, since m∠SRT + m∠TRU = 90° and since m∠SRT = (x + 15)°,(x+15)°+m∠TRU = 90°.
Thus m∠TRU = 90°−(x + 15)°, or (75 − x)°.
For all numbers x and y, let the operation ¤ be defined as x ¤ y = 2xy − 4x. If a and b are positive integers, which of the following can be equal to zero?
I. a ¤ b
II. (a − b) ¤ b
III. b ¤ (a − b)
-
Solution
To solve this problem, substitute a for x and b for y and set it equal to zero: 2ab − 4a = 0. Factor out 2a: 2a(b − 2) = 0. Since a cannot equal zero (it must be positive), then (b − 2) = 0. Solving for b gives you b = 2. Since b is an integer, Roman Numeral I can equal 0. Eliminate answer choices B and C. Substitute (a − b) for x and b for y and set it equal to zero: 2(a − b)b − 4(a − b) = 0. Factor out 2(a − b): 2(a − b)(b − 2) = 0. This is true if a = b or if b = 2. Since a or b can be an integer, Roman Numeral II can equal 0. Eliminate answer choice A. Substitute b for x and (a − b) for y and set it equal to zero: 2b(a − b) − 4b = 0. Factor out 2b: 2b[(a − b) − 2] = 0. Since b cannot equal zero (it must be positive), then (a − b − 2) = 0. Solving for a gives you a = b + 2, which can be an integer. Solving for b gives you b = 2 − a, which can be an integer. So, Roman Numeral III can equal 0. Eliminate answer choice D. Each of the Roman Numerals can be equal to zero.
What is the median of the following 6 test scores?
64, 72, 85, 80, 72, 89
-
Solution
The median is the middle value of a list of values that are in ascending or descending order. First, put the test scores in order: 64, 72, 72, 80, 85, 89. Because there are six values, the median will be the average of the middle two values: \(\frac{72 + 80}{2}=\frac{152}{2}\) , or 76.
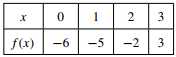
The table above gives values of the quadratic function f for selected values of x. Which of the following defines the quadratic function f ?
-
Solution
To solve this problem, substitute the given values for x into each function to see if you get the correct value for f (x). Answer choice A is correct because for each of the four given x values, x2 − 6 yields the correct f (x) values.