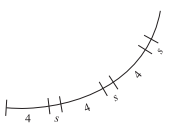
he figure below shows part of a circle whose circum ference is 40. If arcs of length 4 and length s continue to alternate around the entire circle so that there are 8 arcs of each length, what is the degree measure of each of the arcs of length s?

F. 6◦
G. 9◦
H. 12◦
J. 18◦
K. 36◦

Solution

First, find the value of s. Since there are 8 arcs of each length, it follows that there are 8 arcs of length (4 + s). Since the circumference is 40, then 8(4 + s) = 40. Solve for s: 32 + 8s = 40 and s = 1. Now that you know the value of each length, you can solve for the degree measure of each of the arcs of lengths. You know that the entire circle has 360◦. You also know that the length of the smaller arc (s) is ¹⁄₄ the length of the larger arc. Therefore, you can set up the following equation: 8x + 8¹⁄₄x = 360◦, where x is the degree measure corresponding to each arc of length 4 and ¹⁄₄x is the degree measure corresponding to each arc of length s = 1. Now you have 8x + 8 ¹⁄₄x, or 8x + 2x, which is 10x = 360◦. So x = 36◦. Recall that x is the degree measure corresponding to each arc of length 4. The degree measure corresponding to each arc of length s is ¹⁄₄x;¹⁄₄(36) = 9◦.

Which of the following is always equal to y(3 − y) + 5(y − 7) ?

A. 8y − 35
B. 8y − 7
C. −y² + 8y − 7
D. −y² + 8y − 35
E. 8y³ − 35

Solution

To solve this problem, you must distribute correctly and remember the proper signs. When you distribute y(3−y)+5(y−7), you arrive at 3y − y² + 5y − 35. Once you add like terms, you get −y² + 8y − 35.

If 6x − 5 = 3x − 16, then x = ?

F. −11
G. −7
H. -$\frac{11}{3}$
J. $\frac{11}{3}$
K.

Solution

To solve this problem, since the equations equal each other, you must combine like terms and solve for x:

6x − 5 = 3x − 16

6x − 5 − 3x = 3x − 16 − 3x

3x − 5 + 5 = −16 + 5

$\frac{3x}{3}=-\frac{11}{3}$

x =$-\frac{11}{3}$

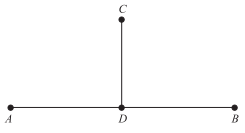
In the figure below, D is a point on segment AB, and the segment CD is perpendicular to the segment AB. Based on this information, which of the following conclusions can be made?

A. Point C is equidistant from A to B.
B. Segments AD and DB are equal in length.
C. The segment CD bisects the segment AB.
D. Angle CDA is larger than angle CDB.
E. Angle CDA is congruent to angle CDB.

Solution

Remembering that perpendicular lines form right angles, the angles CDA and CDB both measure 90◦ and thus are equal in measure, answer choice E. From the figure it may appear as if segments AD and DB are equal in length, but that cannot be determined based solely on the information given in the problem.

The price of a cantaloupe is directly proportional to its weight. If a cantaloupe that weighs 3.0 pounds costs $3.87, approximately how much will a 2.25-pound cantaloupe cost?

F. $2.90
G. $2.65
H. $2.25
J. $1.87
K. $1.29

Solution

If 3(a − 6) = −21, then a = ?

A. −9
B. −³⁄₂
C. −1
D. ⁷⁄₃
E. 5

Solution

Given that 3(a−6)=−21:

$\frac{3(a − 6)}{3}=\frac{-21}{3}$

(a − 6) + 6 = −7 + 6

a = −1

What is the volume, in cubic inches, of a cube whose edges each measure 5 inches in length?

F. 15
G. 25
H. 50
J. 125
K. 500

Solution

The volume of a cube is calculated by multiplying the length by the width by the height. Because each side of a cube is congruent, simply calculate (side)³. Therefore, the volume is 5³, or 125.

As part of a school report on the cost of gasoline, Raquel wants to find the average cost of purchasing a gallon of regular unleaded gasoline from local gas stations. She surveys 4 stations and finds the cost per gallon of regular unleaded gas from the 4 stations to be $2.45, $2.50, $2.49, and $2.56, respectively. Using this data, what is the average cost of purchasing one gallon of regular unleaded gasoline from these 4 gas stations?

A. $2.55
B. $2.53
C. $2.50
D. $2.49
E. $2.45

Solution

To compute the average of the four prices per gallon of gasoline, add the four prices and divide that sum by the number of prices, which in this case is four:
$\frac{\$ 2.45 +\$ 2.50 +\$ 2.49 +\$ 2.56}{4}=\frac{10}{4},\$ 2.50$

Disregarding sales tax, how much will you save when you buy a $12.00 video that is on sale for 20% off?

F. $0.24
G. $0.48
H. $1.20
J. $2.40
K. $3.60

Solution

To find how much money you save when you buy a $12 video that is on sale for 20% off, you should find 20% of $12. To do so, multiply $12 by 20%, or 0.20; ($12)(0.20) = $2.40.

The lowest temperature on a winter morning was −7 ◦F. Later the same day the temperature reached a high of 21◦F. By how many degrees Fahrenheit did the temperature increase?

A. 32
B. 28
C. 21
D. 14
E. 7

Solution

To find how many degrees Fahrenheit the temperature increased, you need to find the range between the highest and lowest temperature for the day. To do so, subtract the lowest temperature from the highest temperature: 21 − (−7) = 21 + 7 = 28 degrees Fahrenheit. If you chose D, you may have forgotten that subtracting a negative number is the same thing as adding that number.

Attempted

0

Correct

0

Wrong

0

Complete