If x + 2⁄3 = \(\frac{8}{21}\) , then x = ?
-
Solution


If m > 0 and n < 0, then m − n:
-
Solution
Although the exact values of m and n are not known, it can be determined that the difference of m and n is always positive. This is true because subtracting a negative number is the same as adding the positive. Since n < 0, subtracting the negative n will always be a net addition to the value of m, which is a positive number to begin with. Therefore, answer choice A is correct.
On the blueprint for Roger’s house, DO YOUR FIGURING HERE. 1⁄4 inch represents an actual length of 1 foot. What is the area, in square feet, of Roger’s rectangular living room, which is 3 inches by 41⁄4 inches on the blueprint?
-
Solution
Since 1⁄4 inch on the blueprint represents an actual length of 1 foot, 1 inch on the blue print represents an actual length of 4 feet. When the room is 3 inches by 41⁄4 inches on the blueprint, it is actually 4(3) feet by 4(41⁄4) feet. Because the room is rectangular, the area is equal to length times width, so the area is 4(3) × 4(41⁄4)= 12 × 17 = 204 square feet.
What is the next term after −1⁄3 in the geometric sequence 9, −3, 1, −1⁄3, …?
-
Solution
To find the next term in the geometric sequence, recall that when looking at a geometric sequence, the nth term can be written (for some base number b) as bn. This sequence is decreasing in magnitude, thus the absolute value of b is less than 1. It also alternates signs, which indicates that b is negative. At this point, mathematical intuition might suggest trying b = −1⁄3, and then calculating for what value of n the terms in the given sequence correspond (see table).

What is the value of the expression 2x3 − x2 + 3x + 5 for x = −2?
-
Solution
To find the value of the expression 2x3 − x2 + 3x + 5 for x = −2, simply substitute −2 into the expression wherever there is an x, as follows:
2(−2)3 − (−2)2 + 3(−2) + 5
2(−8) − (4) + 3(−2) + 5
2(−8) − 4 + (−6) + 5
Recall that when taking negative numbers to odd powers, they retain their negative sign; however, when negative numbers are taken to even powers, they become positive. Thus the expression 2(−8) − 4 + (−6) + 5 is equivalent to −16 − 4 − 6 + 6 = 21.
The circle shown below has a radius of 5 meters, and the length of chord XY is 8 meters. If C marks the center of the circle, what is the length, in meters, of segment CZ?
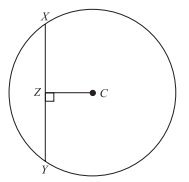
-
Solution
If the length of the chord XY is 8, then the length of the segment XZ is 4. The right triangle XCZ has a hypotenuse of 5 (equal to the radius), leg of 4, and second leg equal to the length of segment CZ. To find the length of segment CZ you can use the Pythagorean Theorem for a right triangle (c2 = a2 + b2 where c is the hypotenuse and a and b are legs):
52 = 42 + CZ2
CZ2 = 52 − 42
CZ2 = 25 − 16
CZ2 = 9
CZ = 3
The speed of a car exceeds twice the speed of a truck by 15 mph. If t is the speed of the truck, which of the following expresses the speed, in miles per hour, of the car?
-
Solution
If t is the speed of the truck, then twice the speed of the truck can be written as 2t. If the speed of the car exceeded twice the speed of the truck by 15 mph, the car’s speed was 2t + 15.
If a board 9 feet 6 inches in length is cut into 2 equal parts, what will be the length of each part?
-
Solution
To find half of 9 feet 6 inches, recall that there are 12 inches in a foot. Therefore, 9 feet 6 inches is equal to 9(12) + 6 = 114 inches. Half of 114 inches is 57 inches, which is equivalent to 4 feet 9 inches [4(12) + 9 = 57].
On the line segment below, the ratio of lengths AB to BC is 1:4. What is the ratio of AB to AC?
![]()
-
Solution
To determine the ratios, it is helpful to assign numerical values to the lengths of the segments. In this case, since the ratio of AB to BC is 1:4, let AB have a length of 1 and BC have a length of 4. Since AC = AB + BC, it can be given a length of 5. Therefore, the ratio of lengths AB to AC is 1:5.
In a poll, 44 people were in favor of constructing a new high school, 58 were against it, and 8 people had no opinion. What fraction of those people polled were in favor of constructing a new high school?
-
Solution
To solve this problem, divide the number of those people in favor of constructing a new high school by the total number of people polled and simplify, as follows:
44 ÷ (44 + 58 + 8) = 44/110 = 2/5


