For the 2 functions f (x) and g(x), tables of values are shown below. What is the value of g ( f (−1))?

-
Solution
To find g(f (x)) using the values of the functions f (x) and g(x) as given in the tables, think of g(f (x)) as applying the function g to f (x). So, first find f (x) for x = −1; f (−1) = 2. Then, find g(x) for x = 2 : g(2) = 3.
Maria posted a time of 37 minutes and 29 seconds for a 5-mile running course. About how many miles per hour did she average during the run?
-
Solution

In the standard (x,y) coordinate plane, what are the coordinates of the midpoint of a line segment with endpoints (−1,3) and (2,5)?
-
Solution

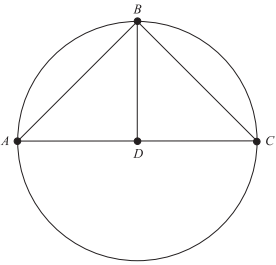
In the figure below, AC is the diameter of the circle, B is a point on the circle, AB is congruent to BC, and D is the midpoint of AC. What is the degree measure of angle ABD?
-
Solution
Since AC is the diameter of the circle, and D is the midpoint of AC, D is the center of the circle. Thus the distance from D to any point on the circle is equal to the radius, r. Since B is a point on the circle, the distance BD is equal to r. Since A is a point on the circle, the distance AD is also equal to r. Further, since AB is congruent to BC, the segment AB is perpendicular to the segment AD, thus the measure of angle ADB is 90◦. In the triangle ABD, two sides are equal to r, thus the triangle is isosceles with one of the angles equal to 90◦. The other two angles are then equal in measure and add up to 90◦. Therefore, angle ABD has a measure of 45◦
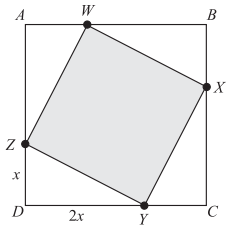
Sides \(\overline{AB}\) , \(\overline{BC}\), \(\overline{CD}\), and \(\overline{DA}\) of square ABCD are broken up by points W, X, Y, and Z as shown below. If \(\overline{AB}\) is 6 inches long, what is the area, in square inches, of the shaded region?
-
Solution
When square ABCD is divided as shown, each of the small triangles has legs of length 2 and 4. They also happen to be right triangles, because each shares one angle with the corner of the large square, which are right angles. To solve for the area of the shaded region, you can use the Pythagorean Theorem to calculate the length of the side of the shaded square. Alternatively, you can find the area of one triangle, quadruple that value, and subtract it from the area of square ABCD, which is 62, or 36 square inches.
The area of a triangle is equal to 1⁄2(base)(height). In a right triangle, either leg will work as the value for the base or the height, so the area of one triangle is A = 1⁄2(2)(4) = 4. The area of the 4 triangles together, then, is 4 × 4, or 16. Thus the area of the shaded region is 36 − 16, or 20.
ΔABC is similar to ΔXYZ. AB is 5 inches long, BC is 8 inches long, and AC is 3 inches long. If the longest side of ΔXYZ is 20 inches long, what is the perimeter, in inches, of ΔXYZ?
-
Solution
When AB is 5 inches long, BC is 8 inches long, and AC is 3 inches long, ABC has a perimeter of 5 + 8 + 3 = 16. To find the perimeter of XYZ when its longest side is 20, you can set up proportions to find the lengths of the sides, since the sides of similar triangles are in proportion to each other. In this case, you can take the proportion of the longest sides, 20:8, and apply it to the perimeter p:
\(\frac{20}{8}=\frac{p}{16}\)
P = \(\frac{20 \times 16}{8}=40\)
-
Solution

If x is any number other than 3 and 6, then \(\frac{(x − 3)(x − 6)}{(3 − x)(x − 6)}\)?
-
Solution

If sin A = 3⁄5, then which of the following could be tan A?
-
Solution
Given that sin A = 3⁄5,you might want to draw a picture like the one below to illustrate the situation.

In this case, the ratio of the side opposite angle A to the hypotenuse is 3⁄5. To find tan A, the length of the other leg is needed. This can be obtained using the Pythagorean Theorem, or by knowing that this is a special 3–4–5 right triangle. According to the Pythagorean Theorem (in a right triangle with sides a, b, and c, where c is the hypotenuse, c2 = a2 + b2), 52 = 32 + x2, where x is the length of the unknown leg. Solve for x:
x2 = 52 − 32
x2 = 25 − 9
x2 = 16
x = 4
Once the length of the third leg is obtained, tan A = \(\frac{opposite}{adjacent}\) = 3⁄4.
In Mrs. Hartley’s foreign language class, students must take both a written exam and an oral exam. In the past, 85% of her students passed the written exam and 70% of those who passed the written exam also passed the oral exam. Based on these figures, about how many students in a random group of 100 students would you expect to pass both exams?
-
Solution
The percent of students who pass both exams is (85%)(70%), or 0.85 × 0.70, which is 0.595. In a sample of 100, 100 × 0.595, or 59.5 (roughly 60) students would be expected to pass both exams.




