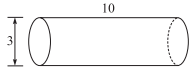
A formula for the volume, V, of a right circular cylinder is V = πr2h, where r is the radius and h is the height. If a tanker truck has a tank as shown below with a diameter of 3 meters and a length of 10 meters and is filled with water, then the weight, in pounds, of the water cargo is: (Note: 1 cubic meter of water weighs approximately 2,205 pounds.)
-
Solution
The diameter of the cylinder is 3 meters.
Therefore, the radius is 1.5 meters.
Using the formula for the volume of a right circular cylinder, V = πr2h with h equal to the length 10 meters, V = π(1.5)2(10), or approximately 70.65 cubic meters.
Since water weighs about 2,205 pounds per cubic meter, the weight of the water cargo is 2,205 × 70.65, or about 156,000 pounds
In the standard (x,y) coordinate plane, what is the distance between the points (4,−7) and (−1,5)?
-
Solution


Rebecca is trying to schedule volunteers to help at a school carnival. There are 5 one-hour shifts to be filled by 5 different volunteers. If each shift must have one and only one volunteer, how many different arrangements can the schedule have?
-
Solution
Think of each shift as a spot to be filled: __×__×__×__×__.
In each spot there are only a certain number of available workers.
For example, the first spot can have any of the 5 volunteers working, leaving 4 possible workers for the next shift, and so on.
Therefore, the number of possible arrangements of volunteers is 5 × 4 × 3 × 2 × 1 = 5!, or 120.
When entering information about the budget of her charity ball, Laura records an expense of $20.00. However, Laura accidentally enters the $20.00 as income instead of an expense. The balance of the charity ball budget now shows:
-
Solution
Because Laura recorded the $20 as income, the balance of the budget would appear to be $20 higher than it should be. However, because the $20 was an expense, once the $20 was deducted from the income statement and then deducted again from the expense report, the balance would appear to be $40 more than it should.
If |x| = x + 12, then x = ?
-
Solution
Recall that |x| means “absolute value of x,” which is the magnitude of a number, regardless of its sign. For instance |−2|=|2| = 2. In the case of this problem, the equation |x| = x + 12 can be broken into 2 related sub-equations: x = x +12 and −x = x +12. When x = x + 12, the equation does not make sense because if you subtract x from both sides, 0 = 12 remains, which obviously is false. With the other sub-equation, −x = x + 12, you can subtract an x from both sides to get −2x = 12. Dividing by −2, you arrive at x = −6
What fraction lies exactly halfway between 1⁄3 and 1⁄2?
-
Solution
To solve this problem, convert 1⁄3 and 1⁄2 to fractions with a common denominator, such that 1⁄3 = 2⁄6 and 1⁄2 = 3⁄6. The halfway point will be somewhere between 2⁄6 and 3⁄6. From there, you can increase the magnitude of the denominator so that a halfway point between the numerators is more evident.1⁄3= 2⁄6 = \(\frac{4}{12}\) and 1⁄2 = 3⁄6 = \(\frac{6}{12}\). Thus the halfway point is between \(\frac{4}{12}\) and \(\frac{6}{12}\), which is \(\frac{5}{12}\).
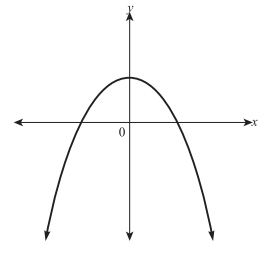
The graph of y = ax2 + bx + c in the standard (x,y) coordinate plane is shown below. When y = 0, which of the following best describes the solution set for x?
-
Solution
In a graph, the values at which y = 0 will be where the graph of a function crosses the x-axis. As seen in the figure, the graph of y = ax2 + bx + c crosses the x-axis twice; thus there will be two real solutions for the equation 0 = ax2 + bx + c. Imaginary solutions would apply if the graph did not cross the x-axis at any point.
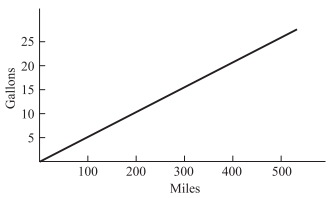
The line graphed below shows the predicted gasoline use for a certain truck. Which of the following is the closest estimate of this truck’s predicted rate of gasoline use, in miles per gallon?
-
Solution
To find the rate of gasoline use, which translates into miles per gallon, divide the number of miles traveled by the number of gallons of gasoline used. In this case, you can see that the graph goes through the point (100,5), (200,10) and so on. Based on this information, the rate would be \(\frac{100 miles}{5 gallons}\) , or 20 miles per gallon.
The formula for the area of a trapezoid is A = 1⁄2h (b1 + b2), where b1 and b2 are the lengths of the two parallel sides and h is the height. Which of the following is an expression for b1?
-
Solution
To solve A = 1⁄2h(b1 + b2)
for b1, divide both sides by h and multiply both sides by 2.
The remaining equation is 2A⁄h = b1 + b2.
Then simply subtract b2 from both sides of the equation to get b1 = 2A⁄h − b2.
For positive real numbers x, y, and z, which of the following expressions is equivalent to x1⁄2y3⁄4z5⁄8?
-
Solution



