What is the slope of a line that is perpendicular to the line determined by the equation 5x + 8y = 17?
-
Solution
The line 5x + 8y = 17 is given in standard form. You should find the slope of this line by converting the equation into slope-intercept form (y = mx + b, where m is the slope and b is the y-intercept):
5x + 8y = 17
8y = −5x + 17
y =\(\frac{−5x}{8}+\frac{17}{8}\)
Since the equation is now in slope-intercept form, it is easy to see that the slope of the line is −5⁄8. The slope of a line perpendicular to the line with a slope of −5⁄8 is 8⁄5, answer choice K (remember that perpendicular lines have negative reciprocal slopes).
If the volume of a cube is 64, what is the shortest distance from the center of the cube to the base of the cube?
-
Solution
To solve this problem, you must realize that the volume of a cube is equal to (length)(width)(height) or simply (side)3, since all sides of a cube are equivalent in length.
To find the length of one side, find the cube root of 64,which is 4.
(43 = 64) Because all sides of a cube are equal, the shortest distance from the center of the cube to the base of the cube will equal the midpoint of the length of the cube, which is 4⁄2, or 2.
For which of the following values of c will there be 2 distinct real solutions to the equation 5x2+16x+ c = 0?
-
Solution
The best way to solve this problem is to plug in the answer choices for c, and factor the equation, starting with answer choice F:
5x2 + 16x + 3 = 0
(5x + 1)(x + 3) = 0
5x + 1 = 0, x = −1⁄5
x + 3 = 0; x = −3
Answer choice F gives you 2 distinct solutions for x, so you do not need to try the remaining answer choices. Using the quadratic formula to solve the other choices will not give you real solutions.
If a is inversely proportional to b and a = 36 when b = 12, what is the value of a when b = 48?
-
Solution
By definition, if a and b are inversely proportional, then a1b1 = a2b2.
Therefore, (36)(12) = (48)a. Solve for a as follows:
(36)(12) = (48)a
432 = 48a
9 = a
For values of x where sin x , cos x, and tan x are all defined, \(\frac{(cos x)}{(tan x)(sin x)}\)=?
-
Solution

Which of the following is (are) equivalent to the mathematical operation a(b − c) for all real numbers a, b, and c?
I. ca − ba
II. ab − ac
III. (b − c)a
-
Solution
This question tests your ability to recognize and apply the distributive property of multiplication. According to the distributive property, for any numbers a, b, and c, a(b − c) = ab − ac.
a(b − c) = ab − ac, which is NOT equivalent to ca − ba, so Roman Numeral I is incorrect; eliminate answer choices B, C, and E.
ab - ac, so Roman Numeral II is correct.
(b − c)a, so Roman Numeral III is also correct.
Since II and III are equivalent to a(b − c), answer choice D is correct.
If x2 − 45b2 = 4xb, what are the 2 solutions for x in terms of b?
-
Solution
The first step in answering this question is to set x2 −45b2 = 4xb equal to zero, by isolating all of the terms on the left side:
x2 − 4xb − 45b2 = 0
The next step is to factor the equation and set each group equal to 0 in order to solve for x:
(x + 5b)(x − 9b) = 0
x + 5b = 0, so x = −5b
x − 9b = 0, so x = 9b
The two solutions for x are −5b or 9b.
It is estimated that, from the beginning of 1993 to the end of 1997, the average number of CDs bought by teenagers increased from 7 per year to 15 per year. During the same time period, the average number of video games purchased by teenagers increased from 6 per year to 18 per year. Assuming that in each case the rates or purchase are the same, in what year did teenagers buy the same average number of CDs and video games?
-
Solution
The best way to solve this problem is to set up a table indicating the time period in years and the number of both CDs and video games purchased during the years given. The rate of purchase is the same, so, based on information in the problem, you can fill in the table below.

Teenagers bought the same average number of CDs and video games in 1994.
The figure below is a regular hexagon. What is the measure of one of the interior angles of the hexagon?
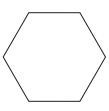
-
Solution
To solve for the total measure of all interior angles of a regular polygon, use the formula (n−2)(180°) where n is the number of vertices of the polygon. A regular hexagon has 6 vertices, so the total measure of all interior angles is (6 − 2)(180) = (4)(180) = 720°. Since there are six interior angles, each one is \(\frac{720^{\circ}}{6}\)= 120°.
In the figure below, line AB is parallel to the base of the triangle and creates a smaller triangle inside of the original triangle. If the lengths of segments are as shown and the smaller triangle has an area of 8 cm2, what is the area, in centimeters, of the original triangle?
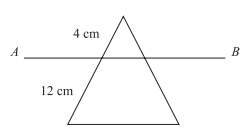
-
Solution
Since the two lines are parallel, the two triangles are similar and share the same constant ratio.
The smaller triangle has one side with a length of 4 cm, and the larger triangle has one side with a length of 4 + 12, or 16 cm.
The legs of the triangles have a ratio of 4:16, which can be reduced to 1:4.
The ratio of 1:4 also extends to the area of the triangles.
You are given that the smaller triangle has an area of 8cm2.
The larger triangle has an area that is 4 times larger, so the area of the larger triangle is 4 × 8 = 32 cm2.

