If a, b, and c are consecutive positive integers and 2a × 2b × 2c = 512, then 2a + 2b + 2c =?
-
Solution
To solve this problem, it might be helpful to make a list of the powers of 2: 21 = 2, 22 = 4, 23 = 8, 24 = 16, 25 = 32, and so on. Select consecutive values from this list and multiply them, starting with the values that make the most sense. For example, you know that 2 × 4 × 8 will be less than 512, so try 4 × 8 × 16, which does equal 512. Now, add those same terms: 4 + 8 + 16 = 28.
The area of the trapezoid below is 24 square inches, the altitude is 3 inches, and the length of one base is 5 inches. What is the length, b, of the other base, in inches?
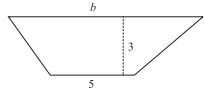
-
Solution
To solve this problem, use the formula for the area of a trapezoid,1⁄2h(b1+b2), where h is the altitude (height) and b1 and b2 are the bases. In this case, the altitude (height) is 3 and one of the bases is 5. Because the area is known to be 24, the other base can be determined by using the equation 24 =(1⁄2)(3)(b + 5). Dividing both sides of the equation by 3⁄2 (or multiplying both sides of the equation by 2⁄3) yields 16 = b + 5, or b = 11.
If the function f satisfies the equation f (x + y) = f (x) + f (y) for every pair of real numbers x and y, what is (are) the possible value(s) of f (1)?
-
Solution
If the function f satisfies the equation f (x+y) = f (x)+f (y) for every pair of real numbers x and y, then f is a linear function. For some unknown linear function f , the value of f (1) can be any real number (think of all the possible lines that can be drawn).
If the circumference of a circle is 4⁄3π inches, how many inches long is its radius?
-
Solution
To solve this problem, recall that circumference is 2πr, where r is the radius. If a circle has a circumference of (4⁄3)π, then (4⁄3)π = 2πr. Therefore, 2r = 4⁄3, or r = 2⁄3.
For all x > 4,\(\frac{4x − x^{2}}{x^{2} − 2x − 8}\)?
-
Solution

In ABC below, points B, D, and C are collinear. Segment AB is perpendicular to segment BC, and segment AD bisects angle BAC. If the measure of angle DCA is 60°, what is the measure of angle ADB?
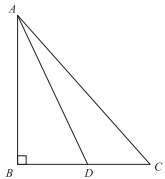
-
Solution
If the measure of angle DCA is 60°, then the measure of angle BCA is 60° as well. Because the angles in a triangle have the sum of 180°, angle BAC is 180 − 90 − 60, or 30°. Because the segment AD bisects angle BAC, angle BAD is equivalent to angle DAC, which is \(\frac{30^{\circ}}{2}\) , or 15°. Further, since the triangle ABD is a right triangle, the measure of angle ADB = 180 − 90 − 15, or 75°.
For what nonzero whole number k does the quadratic equation y2+2ky+4k = 0 have exactly one real solution
for y?
-
Solution
To solve this problem, recall that a quadratic equation has exactly one real solution when the solution is a “double zero.” Such an equation would have the factored form of (y + b)2 = 0, where b is a real number. When you expand the equation, it becomes (y + b)2 is y2 + 2by + b2. The equation y2 + 2ky + 4k = 0 has a similar form; however, in order for the term 4k to represent b2, k must equal 4.
You have enough material to build a fence 120-feet long. If you use it all to enclose a square region, how many square feet will you enclose?
-
Solution
Enclosing a square region with 120 feet of fence would make each side of the square \(\frac{120}{4}\) , or 30 feet. Therefore, the number of square feet enclosed is the area of the region, which would be 302, or 900 square feet.
For the triangle shown below, what is the value of tan x?
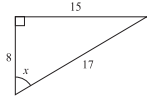
-
Solution
The tangent of an angle is the ratio of the side opposite the angle to the side adjacent to the angle. The side opposite angle x is 15 and the side adjacent is 8, making tan x = \(\frac{15}{8}\).
A circle in the standard (x, y) coordinate plane has center (−4,5) and radius 5 units. Which of the following equations represents this circle?
-
Solution
To solve this problem, you must recall that a circle with center (h, k) and radius r has the equation (x − h)2 + (y − k)2 = r2. A circle that has center (−4, 5) and radius 5 units would therefore have an equation (x + 4)2 + (y − 5)2 = 25.
