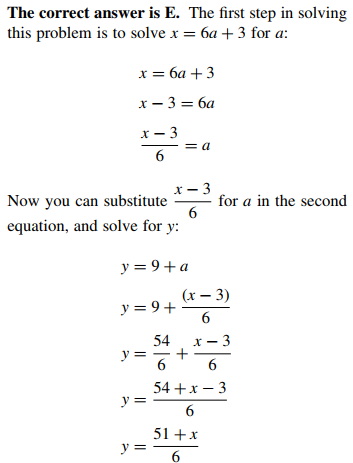For any real number a, the equation |x − 2a| = 5. On a number line, how far apart are the 2 solutions for x?
-
Solution
The absolute value of a number is indicated when a number is placed within two vertical lines. Absolute value can be defined as the numerical value of a real number without regard to its sign. This means that the absolute value of 10, |10|, is the same as the absolute value of −10, | − 10|, in that they both equal 10. If the absolute value of x−2a = 5, then x−2a must also equal −5. If x − 2a = 5, then x = 2a + 5. If x − 2a = −5, then x = 2a − 5. These equations are represented on the number line as follows:

So, the distance apart on the number line is 5 + 5, or 10.
A wheel 27 inches in diameter rolls along a line. How many inches does the wheel roll along the line in 32 revolutions?
-
Solution
When a wheel makes one revolution that means that it goes completely around one time. The distance one time around a wheel is equal to the wheel’s circumference.A wheel is a circle, and the formula for the circumference of a circle is C = 2πr. If the diameter of the wheel is 27, then one time around, or one revolution, of the wheel is equal to 27, which is equal to 2r. So, the circumference of the wheel is 2rπ, or, 27π. Since the wheel made 32 revolutions, multiply 32 by 27π to get 864π.
Carol has an empty container and puts in 6 red chips. She now wants to put in enough white chips so that the probability of drawing a red chip at random from the container is 3⁄8. How many white chips should she put in?
-
Solution
Probability refers to the likelihood of something happening. How many white chips should Carol put into the container so that she is likely to draw 3 red chips every eight draws? Try the answer choices.
F: If she puts in 3 white chips, then the probability of drawing a red chip is 6 (red chips) out of 9 (total chips). Eliminate answer choice F.
G: If she puts in 6 white chips, then the probability of drawing a red chip is 6 (red chips) out of 12 (total chips). Eliminate answer choice G.
H: If she puts in 8 white chips, then the probability of drawing a red chip is 6 (red chips) out of 14 (total chips). Eliminate answer choice H.
J: If she puts in 10 white chips, then the probability of drawing a red chip is 6 (red chips) out of 16 (total chips), which is equivalent to 3 out of 8, or 3⁄8. She should add 10 white chips
For all real integers, which of the following is always an even number?
I. x3 + 4
II. 2x + 4
III. 2x2 + 4
-
Solution
Integers can be even or odd, and positive or negative. Pick real numbers to substitute into the expressions in each Roman Numeral, then eliminate any Roman Numerals that do not always yield and odd number. Whenever a number is multiplied by 2, the result is always even. Thus, II and III are true; answer choice E is correct.
In the figure below, sin α =?
-
Solution
The sine of any acute angle is calculated by dividing the length of the side opposite to the acute angle by the hypotenuse (sin =\(\frac{opp}{hyp}\)). It may help you to draw a diagram to solve this problem, as shown below:

Use the Pythagorean Theorem to calculate the length of the hypotenuse.
a2 + b2 = c2
42 + 42 = c2
16 + 16 = c2
32 = c2
\(\sqrt{32}\) = c
\(\sqrt{32}\) = c
4 √2 = cSo, the sine of angle α is \(\frac{4}{4\sqrt{2}}\) , which can be reduced to 1⁄√2. Recall that roots should be elimnated from denominators:\(\frac{1}{\sqrt{2}}\frac{(\sqrt{2})}{(\sqrt{2})}=\frac{\sqrt{2}}{2}\).
The total weekly profit p, in dollars, from producing and selling x units of a certain product is given by the function p(x) = 225x−(165x+c), where c is a constant. If 75 units were produced and sold last week for a profit of $3,365, what is the value of c?
-
Solution
To solve this problem, substitute the given values into the given equation:
3365 = 225(x) − (165x + c)
You know that 75 units were sold, so set x equal to 75 and solve for c:
3365 = 225(75) − (165(75) + c)
3365 = 16875 − (12375 + c)
3365 = 16875 − 12375 − c
3365 − 4500 = −c
1135 = c
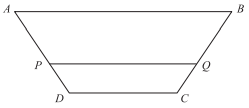
ABCD is a trapezoid that is bisected by line PQ, which is parallel to lines AB and DC. If the length of line DP is 8 units, the length of line PA is 12 units, and the length of line AB is 36 units, what is the length of PQ?
-
Solution
In a trapezoid, the bases are parallel, so AB||DC. You are given that PQ||AB||DC. By definition, the ratio of the length of DP to the length of PA is the same as the ratio of PQ to AB. In other words:
\(\frac{DP}{PA}=\frac{PQ}{AB}\)
Substitute the lengths that are given for DP, PA, and AB and solve for PQ:
\(\frac{8}{12}=\frac{PQ}{36}\)
36 × \(\frac{8}{12}\) = PQ
3 × 8 = PQ
24 = PQ
If x = 6a + 3 and y = 9 + a, which of the following expresses y in terms of x?
-
Solution

For which values of x will 3(x + 4) ≥ 9(4 + x)?
-
Solution
To answer this question, solve the inequality for x, as follows:
3(x − 4) ≥ 9(4 + x)
3x + 12 ≥ 36 + 9x
− 6x ≥ 24
x ≤ −4
Remember that the direction of the sign in an inequality switches when dividing by a negative number.
If 30% of x equals 60% of y, which of the following DO YOUR FIGURING HERE. expresses y in terms of x ?
-
Solution
You are given that 30% of x equals 60% of y, which can be expressed mathematically as 0.3x = 0.6y. To express y in terms of x, solve for y, as follows:
0.3x = 0.6y
0.3x/0.6 = y
0.5x = y
This is equivalent to the expression y = 50% of x.