Math Solved Practice Test Practice Test 53

Rectangle PQRS lies in the standard (x, y) coordinate plane so that its sides are not parallel to the axes. What is the product of the slopes of all four sides of rectangle PQRS?

F. −2
G. −1
H. 0
J. 1
K. 2

Solution

Since the figure is a rectangle, the adjacent sides are perpendicular.

Perpendicular lines have slopes that are negative reciprocals of each other, meaning that the product of their slopes is −1.

Since there are four lines and four perpendicular angles, the product of the slopes
is (−1) × (−1) × (−1) × (−1) = 1

In the standard (x, y) coordinate plane, point B with coordinates (5,6) is the midpoint of AC, and A has coordinates (6,7). What are the coordinates of C?

A. (11,13)
B. (7,8)
C. (4,5)
D. (5.5,6.5)
E. (−4,−8)

Solution

One way to solve this problem is to sketch the (x, y) coordinate plane and plot the given points, as shown below:

A quick glance at the figure and the answer choices should indicate that point C would likely have coordinates (4,5) because none of the other options match the figure.

Use the midpoint formula to calculate the coordinates, as follows:

$5=\frac{(6 + x)}{2}\: \: \: \: \: 6=\frac{(7 + y)}{2}$
10 = 6 + x 12 = 7 + y
4 = x 5 = y

The 6 consecutive integers below add up to 513.

n − 2

n − 1

n + 1

n + 2

n + 3

What is the value of n?

F. 48
G. 53
H. 64
J. 85
K. 86

Solution

One way to solve this problem is to simply set up the equation and solve for n, as follows:

(n − 2) + (n − 1) + n + (n + 1) + (n + 2) + (n + 3) = 513

6n − 2 + (−1) + 1 + 2 + 3 = 513

6n − 3 + 6 = 513

6n + 3 = 513

6n = 510

n = 85

Blair expects an increase of 3% in her current annual salary of $42,000. What would her new annual salary be?

A. $42,003
B. $42,126
C. $43,260
D. $45,000
E. $54,600

Solution

A quick way to solve this problem is to multiply Blair’s current salary by 1.03, which will yield her new salary with a 3% raise (remember, the decimal equivalent of 3% is .03):

42, 000 × 1.03 = 43, 260

You could also multiply Blair’s current salary by.03, then add the result to her current salary:

42, 000 × .03 = 1, 260

42, 000 + 1, 260 = 43, 260

The expression (6n − 5)(n + 4) is equivalent to:

F. 6n² − 20
G. 6n² − 19n − 20
H. 6n² − 29n − 20
J. 6n² + 19n
K. 6n² + 19n − 20

Solution

To solve this problem, use the FOIL method, as follows:
(6n − 5)(n + 4)
First terms: 6n²
Outside terms: 24n
Inside terms: − 5n
Last terms: − 20
Now, put the like terms in order and simplify:
6n² + 24n − 5n − 20
= 6n² + 19n − 20

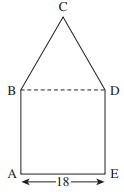
The figure below is composed of square ABDE and equi-lateral triangle BCD. The length of line segment AE is 18 centimeters. What is the perimeter of ABCDE, in centimeters?

A. 48
B. 54
C. 72
D. 90
E. 106

Solution

The perimeter is the distance around an object. You are given that the figure is composed of a square, which has congruent sides,and an equilateral triangle, which has congruent sides. You are also given that the length of one side of the square is 18 cm, which means that the length of each of the remaining sides is also 18. Therefore, the perimeter of ABCDE is 18 × 5 = 90.

x² + 60x + 54 − 59x − 82x² is equivalent to:

F. −26x²
G. −26x⁶
H. −81x² + x + 54
J. −81x² − x + 54
K. −83x² − x − 54

Solution

To solve this problem, add or subtract like terms, as follows:
x² + 60x + 54 − 59x − 82x²
= (−82x² + x²) + (60x − 59x) + 54
= −81x² + x + 54

Runner A averages 5 miles per hour, and Runner B averages 6 miles per hour. At these rates, how much longer does it take Runner A than Runner B to run 15 miles?

A. .5 hour
B. 1 hour
C. 1.5 hours
D. 2.5 hours
E. 3 hours

Solution

The first step in solving this problem is to calculate the time it takes each runner to run 15 miles. Use the Distance = Rate × Time formula, as follows (because you are calculating the time, use the variable x):

Runner A takes 3 hours and Runner B takes 2.5 hours to run 15 miles. Therefore, it takes Runner A half an hour (3−2.5 = 0.5) longer to run 15 miles.

An editor charges $30 for each hour he works on a book project, plus a flat $25 editing fee. How many hours of work are included in a $190 bill for a book project?

F. 3²⁄₅
G. 4
H. 5¹⁄₂
J. 6¹⁄₃
K. 7

Solution

To solve this problem, first subtract the flat fee from the total bill:
190 − 25 = 165
The editor billed $165 for his hourly work. Now, simply divide 165 by 30 to determine the number of hours he worked:
165 ÷ 30 = 5.5, or 5¹⁄₂

|9 − 5|−|5 − 9| =?

A. −8
B. −6
C. −4
D. 0
E. 8

Solution

To solve this problem, first perform the operations within the absolute value signs, and then perform the subtraction, as follows:
|9 − 5|−|5 − 9|
= |4|−|− 4|
= 4 − 4 = 0