A formula used to compute the current value of an investment account is A = P(1 + r)ⁿ, where A is the current value, P is the amount deposited, r is the rate of interest for 1 compounding period, expressed as a decimal, and n is the number of compounding periods. Which of the following is closest to the value of an investment account after 3 years if $8,000 is deposited at 5% annual interest compounded annually?

F. $8,400
G. $9,261
H. $15,730
J. $25,200
K. $33,463

Solution

To solve this problem, substitute the given values into the formula as follows:

A = 8, 000(1 + 0.05)³

= 8, 000(1.157625)

= 9, 261

Cube X has an edge length of 2 inches. Cube Y has an edge length triple that of Cube X. What is the volume, in cubic inches, of Cube Y?

A. 6
B. 12
C. 36
D. 72
E. 216

Solution

The volume of a cube is calculated by multiplying the length × width × height.

You are given that Cube X has an edge length of 2. Because Cube Y has an edge length triple that of Cube X, the volume of Cube Y is 6 × 6 × 6, or 6³ = 216 cubic inches.

What is the area of a circle that has a circumference of .5π?

F. 0.0625π
G. 0.10π
H. 0.25π
J. 25π
K. 625π

Solution

To solve this problem, remember that the formula for the circumference of a circle is C=2πr, and the formula for the area of a circle is A = πr², where r is the radius. You are given that the circumference is .5π. Calculate the value of r as follows:

2πr = 0.5π

r = 0.25

Now, substitute 0.25 into the formula for the area and solve:

A = πr²

= π(0.25)²

= 0.0625π

Casey has buckets of 3 different sizes. The total capacity of 12 of the buckets is g gallons, the total capacity of 8 buckets of another size is g gallons, and the total capacity of 4 buckets of the third size is also g gallons. In terms of g when g>0, what is the capacity, in gallons, of each of the smallest-sized buckets?

A. $\frac{g}{12}$
B. ^g⁄₈
C. ^g⁄₄
D. 12g
E. 8g

Solution

To solve this problem,first determine the size of each bucket. Because the total capacity of 12 buckets is g gallons, each bucket can hold ($\frac{1}{12}$)g, or $\frac{g}{12}$ gallons.

Because the total capacity of 8 buckets is g gallons, then each of those buckets can hold (¹⁄₈)g, or ^g⁄₈ gallons.

If the total capacity of 4 buckets is g gallons, then each bucket is (¹⁄₄)g, or ^g⁄₂ gallons.

Therefore, the capacity of the smallest buckets is $\frac{g}{12}$.

If $\frac{4\sqrt{9}}{y\sqrt{11}}=\frac{4\sqrt{9}}{11}$, then y =?

F. 1
G. $\sqrt{11}$
H. 11
J. 22
K. 36

Solution

To solve this problem, note that the numerators are equivalent.

Because this is an equation where the fractions are equal to one another, the denominators must also be equivalent.

Set up an equation for the denominators and solve for y as follows:

y$\sqrt{11}=\sqrt{11}$

y = 11/$\sqrt{11}$

y² = $\left ( \frac{11}{\sqrt{11}} \right )^{2}$

y² = $\frac{121}{11}$ = 11

y = $\sqrt{11}$

You could also have quickly arrived at the correct answer by noticing that $\sqrt{11}$ × $\sqrt{11}$ = 11, so y must equal $\sqrt{11}$

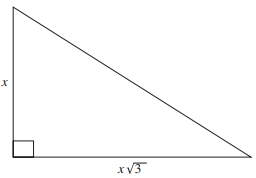
In the figure shown below, the perimeter of the triangle is 15 + 5√3. What is the value of x?

A. 2
B. 3
C. 4
D. 5
E. 6

Solution

A right triangle in which the length of the longer leg is √3 times the length of the shorter leg is a 30°–60°–90° right triangle.

Another property of this type of right triangle is that the hypotenuse is 2 times the length of the shorter leg.

So, this right triangle has lengths x, x√3, and 2x.

Its perimeter is x + x√3 + 2x = 15, or 3x +x√3 = 15+5 √3.

Subtract 5√3 from both sides to get 3x = 15; x = 5.

The fixed costs of printing a certain textbook are $900.00 per week. The variable costs are $1.50 per textbook. Which of the following expressions can be used to model the cost of printing t textbooks in 1 week?

F. $901.50t
G. $150t−$900.00
H. $900.00t+$1.50
J. $900.00−$1.50t
K. $900.00 + $1.50t

Solution

You are given that the fixed costs are $900, which means that the cost of printing will be $900 plus the cost of printing each textbook.

The cost of printing each textbook is determined by multiplying the number of textbooks, t, by the cost per textbook, $1.50.

Therefore, the cost of printing each textbook is 1.50t, and the cost of printing t textbooks in one week is 900 + 1.50t.

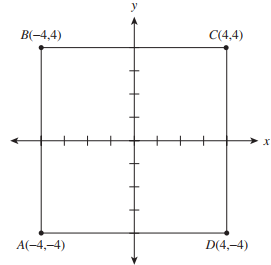
In the square graphed below, what is the slope of line segment AC?

A. 4
B. 2
C. 1
D. −1
E. −4

Solution

Calculate the slope by finding the change in y-values over the change in x-values using the coordinates for points A and C:

$\frac{4 − (−4)}{4 − (−4)}=\frac{8}{8}=1$

What values of a are solutions for a² + 2a = 8?

F. 6 and 8
G. 0 and 2
H. −2 and 4
J. −2 and 0
K. −4 and 2

Solution

To solve this problem, factor the quadratic equation as follows:

a² + 2a − 8 = 0

(a + 4)(a − 2) = 0

a + 4 = 0 a − 2 = 0

a = −4 a = 2

The values of a are −4 and 2.

For all x > 0, the expression $\frac{3x^{3}}{3x^{9}}$ equals:

A. x⁻⁶
B. x³
C. x⁶
D. x¹²
E. x²

Solution

To answer this question, remember that when you divide exponential values with the same base you must subtract the exponents.

Simplify the expression as follows:

$\frac{3x^{3}}{3x^{9}}$

= $\frac{x^{3}}{x^{9}}$

= x⁻⁶

Attempted

0

Correct

0

Wrong

0

Complete