If there are 6 × 1014 oxygen molecules in a volume of 3 × 107 cubic meters, what is the average number of oxygen molecules per cubic meter?
-
Solution
The first step in solving this problem is to recognize that the average will be equivalent to the volume divided by the number of oxygen molecules. Set up the fraction and solve, keeping in mind that when you divide exponential values with the same base you subtract the exponents:
\(\frac{6\times 10^{14}}{3\times 10^{7}}=2\times 10^{7}\)
Which of the following statements is NOT true about the arithmetic sequence 16, 11, 6, 1, …?
-
Solution
The best way to solve this problem is to use the process of elimination.
Remember that you are looking for the answer that is NOT true! First, determine the common difference of the sequence: 16+(−5) = 11; 11+(−5) = 6; 6+(−5) = 1.
The common difference is −5, so eliminate answer choice D.
Now, consider each of the remaining answer choices:
Answer choice A: The common difference is −5, so the fifth term is 1 + (−5) = −4; eliminate answer choice A.
Answer choice B: The sum of the first five terms is 16 + 11 + 6 + 1 + −4 = 30; eliminate answer choice B.
Answer choice C: If the fifth term is −4, the sixth term is −4 + (−5) = −9, and the seventh term is −9 + (−5) = −14.
Answer choice C is correct because it is NOT true.
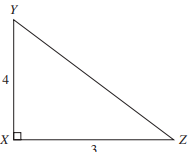
For right triangle XYZ below, what is cos ∠Z?
-
Solution
The first step in solving this problem is to calculate the length of the hypotenuse.
If you recognize that this is a special triangle, you know that the hypotenuse is 5.
You could also let the answer choices guide you,since they each include some combination of 3, 4, and 5.
Otherwise, use the Pythagorean theorem, as follows:
a2 + b2 = c2
32 + 42 = c2
9 + 16 = c2
25 = c2
c = 5
Next, recall that cosine is equal to the length of the adjacent side over the length of the hypotenuse.
Therefore, cos ∠Z is 3⁄5.
In the xy-coordinate system, (√5,s) is one of the points of intersection of the graphs y = 2x2 + 6 and y = −4x2 + m, where m is a constant. What is the value of m?
-
Solution
To find the point of intersection, set the equations equal to each other: 2x2 + 6 = −4x2 + m. Add 4x2 to both sides: 6x2 + 6 = m.
Since the x-coordinate of the point of intersection is √5, then 6(√5)2 + 6 = m and m = 36.
Which of the following is equivalent to the inequality 3x − 6 > 6x + 9?
-
Solution
Inequalities can be solved like equations, by isolating the variable on one side.
Remember, though, that when you multiply an inequality by a negative number, you must reverse the sign:
3x − 6 > 6x + 9
−3x > 15
x < −5
(4x4)4 is equivalent to:
-
Solution
Because the entire value 4x4 is being raised to the 4th power, you must multiply the exponents: 4 × 4 = 16, so (x4)4 = x16.
Therefore, you can eliminate answer choices A, B, and D.
Next, you must raise 4 to the 4th power: 44 = 256, and the correct answer is 256x16.
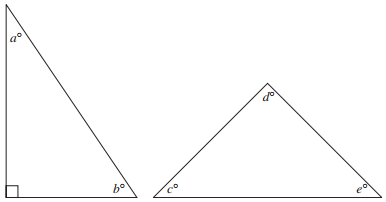
In the triangles shown below, what is the average of angles a, b, c, d, and e?
-
Solution
To solve this problem, first calculate the total measure of all the angles.
The first triangle is a right triangle, which means that a + b = 90°.
The sum of the interior angles of any triangle is 180°, so c + d + e = 180°.
The total measure of the angles, then, is 90° + 180°, or 270°.
Calculate the average: 270° ÷ 5 = 54°.
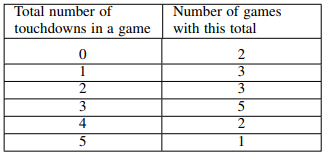
The table below shows the total number of touchdown scored in each of 16 football games during a regular season. What is the average number of touchdowns scored per game, to the nearest tenth?
-
Solution
To solve this problem, first calculate the total number of touchdowns as follows:
2 games with 0 touchdowns = 0 touchdowns
3 games with 1 touchdown = 3 touchdowns
3 games with 2 touchdowns = 6 touchdowns
5 games with 3 touchdowns = 15 touchdowns
2 games with 4 touchdowns = 8 touchdowns
1 games with 5 touchdowns = 5 touchdowns
0 + 3 + 6 + 15 + 8 + 5 = 37 touchdowns
Now, calculate the average number of touchdowns per game.
You are given that there were 16 games,
so the average is 37÷16 = 2.3125, rounded to the nearest tenth is 2.3.
Given f (x) = 3x + 5 and g(x) = x2 − x + 7, which of the following is an expression for f (g(x))?
-
Solution
To solve this problem, substitute the given values into the function as follows:
f (x) = 3x + 5 and g(x) = x2 − x + 7
Therefore, f (g(x)) = f (x2 − x + 7). Substitute x2 − x + 7 for x and solve:
f (g(x)) = 3(x2 − x + 7) + 5 = 3x2 − 3x + 21 + 5 = 3x2 − 3x + 26
A right circular cylinder is shown below, with dimensions given in inches. What is the total surface area of the cylinder, in square inches?
(Note: The total surface area of a cylinder is given by 2πr2 + 2πrh, where r is the radius and h is the height.)

-
Solution
To solve this problem, substitute the given values into the formula as follows:
S = 2πr2 + 2πrh
= 2π(1)2 + 2π(1)(3)
= 8π