Two professors were hired to begin work at the same time. Professor A’s contract called for a starting salary of $50,000 with an increase of $1,500 after each year of employment. Professor B’s contract called for a starting salary of $42,000 with an increase of $2,800 after each year of employment. If y represents the number of full years of employment (that is, the number of yearly increases each professor has received), which of the following equations could be solved to determine the number of years until B’s yearly salary equals A’s yearly salary?

F. 50, 000 + 1, 500y = 42, 000 + 2, 800y
G. 50, 000 + 2, 800y = 42, 000 + 1, 500y
H. 1, 500y + 2, 800y = y
J. 1, 500y + 2, 800y = 42, 000
K. 1, 500y + 2, 800y = 50, 000

Solution

One way to solve this problem is to draw a chart like the one shown below. You are given that y represents the number of full years of employment. Therefore, the salary increase for each professor should be shown as a coefficient of y:

Now that you know how to calculate each professor’s salary after y number of years, set these values equal to each other to come up with the correct equation:

50,000 + 1,500y = 42,000 + 2,800y

If x = −3 and y = 2, then x³y + xy³ =?

A. 78
B. 30
C. −6
D.D. −30trong> −30>D. −30
E. −78

Solution

To solve this problem, simply substitute −3 for x and 2 for y in the equation, as follows (carefully track the negative sign!):

x³y + xy³ = (−3)³(2) + (−3)(2)³

= (−27)(2) + (−3)(8)

= −54 − 24

= −78

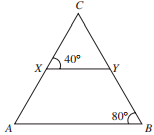
In the figure below, X and Y lie on the sides of ABC, and $\overline{XY}$ is parallel to $\overline{AB}$. What is the measure of ∠C?

F. 120◦
G. 90◦
H. 80◦
J. 60◦
K. 40◦

Solution

To solve this problem you should notice that, because line XY is parallel to line AB, a new triangle, XYC, which is similar to triangle ABC has been created.

Therefore, the corresponding angle measures in each triangle will be congruent, which means that angle A = 40◦.

You are given that the measure of angle B is 80◦.

The sum of the measure of angles in a triangle is 180◦, so set up the following equation to solve for the measure of angle C:

180◦ = 40◦ + 80◦ + C

180◦ = 120◦ + C

60◦ = C

|14|×|− 2| =?

A. −28
B. −16
C. −12
D. 16
E. 28

Solution

To solve this problem, recall that absolute values are always positive.

Therefore, you can ignore the negative sign in front of 2 and solve, as follows:

|14|×|− 2|

= 14 × 2 = 28

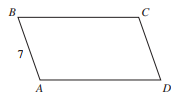
In parallelogram ABCD shown below, AB is 7 inches long. If the parallelogram’s perimeter is 46 inches, how many inches long is AD?

F. 6¹⁄₂
G. 16
H. 28
J. 39
K. 49

Solution

Remember that the perimeter is the distance around an object.

In this case, because the figure is a parallelogram, its perimeter is twice the sum of the lengths of two adjacent sides.

You are given that the length of one side, AB is 7 inches.

Set up the following equation with x as the unknown side length, AD:

46 = 2(7 + x)

46 = 14 + 2x

32 = 2x

16 = x

If 5x + 5 = 25 + 3x, then x =?

A. 2.5
B. 10
C. 20
D. 50
E. 62.5

Solution

Solve this problem by isolating x on the left side of the equation. Perform the following operations:

5x + 5 = 25 + 3x

Subtract 3x from both sides:

2x + 5 = 25

Subtract 5 from both sides:

2x = 20

Divide both sides by 2:

x = 10

What is 1/5 of 16% of $24,000?

F. $160
G. $768
H. $3,840
J. $4,032
K. $7,500

Solution

To solve this problem, first calculate 16% of 24,000, as follows:

24,000 × .16 = 3,840

Next, calculate 1/5 of 3,840, as follows:

3,840 × 1/5

= 3,840 ÷ 5 = 768

Let a function of 2 variables be defined by f (a, b) = ab − (a − b). What is the value of f (8,9)?

A. 89
B. 73
C. 71
D. 34
E. 0

Solution

To solve this problem, substitute 8 for a and 9 for b in the given function and solve, as follows:

f (a, b) = ab − (a − b)

f (8, 9) = (8)(9) − (8 − 9)

= 72 − (−1)

= 72 + 1 = 73

Which of the following expressions is equivalent to (3x + 4)(x − 5)?

F. 3x² + 9x − 9
G. 3x² + 9x + 20
H. 3x² − 19x − 9
J. 3x² − 11x − 20
K. 3x² + 20x − 20

Solution

To solve this problem, use the FOIL method then combine like terms, as follows:

First terms: 3x2

Outside terms: −15x

Inside terms: 4x

Last terms: −20

3x² − 15x + 4x − 20 = 3x² − 11x − 20

One pound is equivalent to 16 ounces. If a book weighs 1.5 pounds, how many ounces, to the nearest tenth, does the book weigh?

A. 10.7
B. 17.5
C. 24.0
D. 61.5
E. 165.0

Solution

To solve this problem, multiply the number of ounces by the number of pounds:

16 × 1.5 = 24

Attempted

0

Correct

0

Wrong

0

Complete