What is the y-coordinate of the point in the standard (x,y) coordinate plane at which the 2 lines y = 3x + 4 and y = 2x + 6 intersect?
-
Solution
You are given that the two lines intersect at a certain point, which means that the lines cross at the same point in the (x,y) coordinate plane, so at that point, the equations of those lines is equal.
Set up the following equation and solve for x:
3x + 4 = 2x + 6
x = 2
Now, substitute 2 for x in either equation and find y, as follows:
y = 3x + 4
y = 3(2) + 4
y = 6 + 4 = 10
What is the least common multiple of 3, 4a, 5b, and 6ab?
-
Solution
Each of the numbers in the values given must divide evenly into the least common multiple.
Therefore, you can quickly eliminate answer choice A because 4 does not divide evenly into 15. Next, notice that each of the number values divides evenly into 60, which is less than 120, so eliminate answer choices D and E.
Because ab is a smaller multiple than a2b, and ab divides evenly into the product of all of the given values, answer choice B is the least common multiple of the given values.
A chord 32 centimeters long is 6 centimeters from the center of a circle, as shown below. What is the radius of the circle, to the nearest tenth of a centimeter?
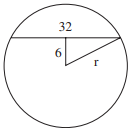
-
Solution
As shown in the figure, the radius, r, is the hypotenuse of a right triangle.
One leg of the triangle is 6 and the other is half of 32, or 16.
Use the Pythagorean theorem to calculate the length of r, as follows:
62 + 162 = r2
36 + 256 = r2
292 = r2
17.08 = r
Rounded to the nearest tenth of a centimeter, r = 17.1 cm
What is the slope-intercept form of 10x − y − 8 = 0?
-
Solution
The slope-intercept form of the equation for a line is y = mx + b; isolate y on the left side of the equation, as follows:
10x − y − 8 = 0
10x − y = 8
− y = −10x + 8
y = 10x − 8
The temperature, t, in degrees Fahrenheit, in a certain city on a certain spring day satisfies the inequality |t − 34| ≤ 40. Which of the following temperatures, in degrees Fahrenheit, is NOT in this range?
-
Solution
One way to solve this problem is to substitute each of the answer choices for t in the inequality to determine which one does NOT work:
Answer choice F: |74 − 34|=|40| = 40;
40 ≤ 40, so eliminate answer choice F.
Answer choice G: |16 − 34|=|− 18| = 18;
18 ≤ 40, so eliminate answer choice G.
Answer choice H: |0 − 34|=|− 34| = 34;
34 ≤ 40, so eliminate answer choice H.
Answer choice J: | − 6 − 34|=|− 40| = 40;
40 ≤ 40, so eliminate answer choice J.
By the process of elimination, answer choice K must be correct: | − 8 − 34|=| − 42| = 42, which is NOT ≤ 40.
If 5 times a number x is subtracted from 15, the result is negative. Which of the following gives the possible value(s) for x?
-
Solution
To solve this problem, first convert the information in the question into its mathematical equivalent, as follows:
5 times a number x = 5x
Subtracting 5x from 15 yields a negative result, so 15 − 5x < 0. Now, solve the inequality for x: 15 − 5x < 0 − 5x < −15 Divide both sides by −5 and reverse the inequality to get x > 3.
Quadrilateral QRST is shown below in the standard (x,y) coordinate plane. For this quadrilateral, QT = 5, RS =\(\sqrt{34}\), ST = 3, and RQ = 6, all in coordinate units.

Which of the following is closest to the perimeter of quadrilateral QRST, in coordinate units?
-
Solution
Recall that the perimeter is the distance around any object.
You are given the side lengths, so start by finding the sum of the given lengths:
QT = 5, RS = \(\sqrt{34}\), ST = 3, and RQ = 6
5 + \(\sqrt{34}\) + 3 + 6
= 14 + \(\sqrt{34}\)
At this point you can safely eliminate answer choices J and K because they are too small.
You are asked for an approximation, so you don’t actually have to do all the math.
The square root of 34 is slightly less than the square root of 36, so the perimeter will be slightly less than 14 + 6 = 20, leaving you with 19.8 as the only viable option.
Quadrilateral QRST is shown below in the standard (x,y) coordinate plane. For this quadrilateral, QT = 5, RS =\(\sqrt{34}\), ST = 3, and RQ = 6, all in coordinate units.

Which of the following are the coordinates of the image of R under a 90◦ counterclockwise rotation about the origin?
-
Solution
To solve this problem, recall that a counterclockwise rotation will move point R to the left about the origin.
Therefore, the x-value will be negative, and you can eliminate answer choices A, B, and C.
Likewise, a rotation about the origin will move point R from its current location, so the x-value will change, leaving answer choice E as the only option.
Quadrilateral QRST is shown below in the standard (x,y) coordinate plane. For this quadrilateral, QT = 5, RS =\(\sqrt{34}\), ST = 3, and RQ = 6, all in coordinate units.

What is the length of QS in coordinate units?
-
Solution
To solve this problem, draw a line from Q to S on the figure, creating right triangle QST.
You are given that the length of QT is 5 and the length of ST is 3.
Use the Pythagorean theorem to find the length of QS, the hypotenuse:
32 + 52 = c2
9 + 25 = c2
34 = c2
\(\sqrt{34}\) = c
In the right triangle shown below, which of the following statements is true about ∠X?
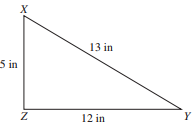
-
Solution
One way to solve this problem is to use SOH CAH TOA to find the sin, cos, and tan of angle X, as follows:
SOH: sin = opposite/hypotenuse = \(\frac{12}{13}\)
CAH: cos = adjacent/hypotenuse = \(\frac{12}{13}\)
TOA: tan = opposite/adjacent = \(\frac{12}{5}\)
Only answer choice B, sin X = \(\frac{12}{13}\), is a true statement about angle X.