What is the largest integer value of t that satisfies the inequality \(\frac{24}{30}\) > \(\frac{t}{24}\)?
-
Solution
One way to solve this problem is to recognize that, in order for \(\frac{24}{30}\) to be greater than \(\frac{t}{24}\), t must be less than 24.
This is true because any fraction with a denominator larger than or equal to its numerator will always be less than a fraction whose numerator is larger than or equal to its denominator.
So, \(\frac{t}{24}\) is only less than \(\frac{24}{30}\) when t is less than 24.
Because you are asked for the largest integer value of t and you know that t must be less than 24, the correct answer must be 19.
You could also set the values equal to each other, cross-multiply and solve for t, as follows:
\(\frac{24}{30}=\frac{t}{24}\)
30t = 576
t = 19.2
The integer value that makes \(\frac{24}{30}=\frac{t}{24}\) greater than \(\frac{24}{30}=\frac{t}{24}\),therefore, is 19.
A circle in the standard (x, y) coordinate plane has center (12,−5) and radius 4 coordinate units. Which of the following is an equation of the circle?
-
Solution
The equation of a circle is (x − h)2 + (y − k)2 = r2, where h and k are the x and y-coordinates of the center of the circle and r is the radius.
Therefore, the equation of the circle centered at point (12, −5) with a radius of 4 is (x − 12)2 + (y + 5)2 = 16.
The hypotenuse of right triangle ABC shown below is 16 inches long. The sine of angle A is \(\frac{3}{5}\). About how many inches long is \(\overline{BC}\)?
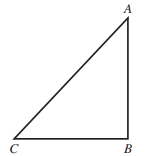
-
Solution
One way to solve this problem is to use SOH CAH TOA for angle A.
You are given that the sine of angle A is 3/5, which means that the ratio of the length of the side opposite angle A to the length of the hypotenuse is 3 to 5.
So, the ratio 3/5 is equal to the ratio BC/AC.
You are given that AC, the hypotenuse, is equal to 16, so now you can set up a proportion, cross-multiply,and solve for BC, as follows:
3/5 = BC/AC
5BC = 3AC
5BC = 3(16)
5BC = 48
BC = 9.6
The costs of carriage rides of different lengths, given in half miles, are shown in the table below:

Each cost consists of a fixed charge and a charge per half mile. What is the fixed charge?
-
Solution
To solve this problem, set the fixed charge to x and set the number of half miles to y.
Now, select two values from the table to create a set of equations, and solve for x and y, as follows:
x + 5y = 8.00
x + 6y = 8.50
The x values will cancel out, leaving y = 0.50,
which means that the cost per half-mile is $0.50; eliminate answer choice A.
Now, substitute.for y in one of the equations to solve for x:
x + 5y = 8
x + 5(.5) = 8
x = 8 − 2.5 = 5.50
If a and b are positive integers such that the greatest common factor of a2b2 and ab3 is 45, then which of the following could b equal?
-
Solution
One way to solve this problem is to recognize that ab2 is a common factor of a2b2 and ab3.
Therefore, it must also be a factor of 45, which can be factored as 5 × 32.
Now you can see that b could be 3, and since there can only be one correct answer, F must be it.
If you test a = 5 and b = 3, you see that the greatest common factor of 52 × 32 and 5 × 33 is 5 × 32, which equals 45.
The ratio of the side lengths for a triangle is exactly 15:14:12. In a second triangle similar to the first, the longest side is 10 inches long. To the nearest tenth of an inch, what is the length of the shortest side of the second triangle?
-
Solution
You are given certain ratios in this problem, so you can set up a proportion to find the length of the shortest side of the second triangle. The ratio of the longest sides of both triangles is \(\frac{15}{10}\).
Set the length of the shortest side of the second triangle to x so that the ratio of the shortest sides of both triangles is \(\frac{12}{x}\).
Now, set up a proportion, cross-multiply, and solve for x:
\(\frac{15}{10}=\frac{12}{x}\)
15x = 120
x = 8
When x/y = 4, x2 − 12y2 =?
-
Solution
You are given that x/y = 4, so x = 4y. Substitute 4y for x in the equation and solve, as follows:
x2 − 12y2
= (4y)
2 − 12y2
= 16y2 − 12y2
= 4y2
The larger of two numbers exceeds twice the smaller number by 9. The sum of twice the larger and 5 times the smaller number is 74. If a is the smaller number, which equation below determines the correct value of a?
-
Solution
To solve this problem, first convert the information given into its mathematical equivalent, as follows (use b to represent the larger number):
The larger of two numbers exceeds twice the smaller number by nine: b = 2a + 9
The sum of twice the larger and five times the smaller number is 74: 2b + 5a = 74
Now, simply substitute the value of b into the second equation in order to solve for a:
2(2a + 9) + 5a = 74
If n = m + 2, then (m − n)4 =?
-
Solution
To solve this problem, first recognize that, if n = m + 2, then m − n = −2.
Now, substitute this value into the second expression and solve:
(m − n)4 = (−2)4 = 16
For x2 ≠ 169,\(\frac{(x − 13)^{2}}{x^{2} − 169}\)=?
-
Solution
To solve this problem, first expand the numerator and factor the denominator, then simplify, as follows:
\(\frac{(x − 13)(x − 13)}{(x − 13)(x + 13)}=\frac{(x − 13)}{(x + 13)}\)