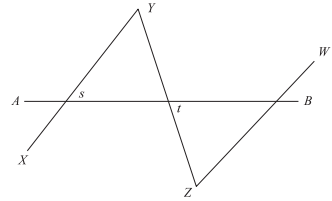
In the figure below, parallel lines XY and ZW are bisected by line AB. If the lengths of XY,YZ, and ZW are the same, and angle t is 45°, then what is the measure of angle s?
-
Solution
Lines XY and ZW are parallel and are bisected by line AB.
As you can see in the diagram from the question, these lines form two triangles.
Because the lines XY, YZ, and ZW are equal, the sides of the triangles that are created are also equal.
The triangle with ∠s is a reflection of the triangle with ∠t, so ∠s = ∠t.
If ∠t = 45°, then ∠s = 45°
| − 2|2 +|− 5| − 3 = ?
-
Solution
This problem requires you to understand absolute value.
Absolute value is the distance of the given value from zero on the number line, without regard to its sign.
So, |−2|2+| − 5| − 3 = 22 + 5 − 3, which is 4 + 5 − 3 = 6.
What is the sum of all the solutions to \(\frac{4x}{x − 1}=\frac{4x}{2x + 2}\)?
-
Solution
The easiest way to solve this problem is to cross-multiply and solve for x:
\(\frac{4x}{x − 1}=\frac{4x}{2x + 2}\)
4x(2x + 2) = 4x(x − 1)
8x2 + 8x = 4x2 − 4x; combine like terms
4x2 + 12x = 0; simplify by factoring out 4x
4x(x + 3) = 0
4x = 0, so x = 0
x + 3 = 0, so x = −3
The two solutions are 0 and –3. The sums of these solutions is 0 + −3, or −3.
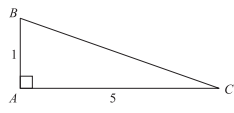
As shown in the figure below, what is the sine of angle C?
-
Solution
The sine of an angle is the length of the opposite side divided by the length of the hypotenuse \(\left ( \frac{opp}{hyp} \right )\).
You are given the measure of the opposite side, but you are not given the hypotenuse.
So you must use the Pythagorean Theorem to find the measure of the hypotenuse:
(1)2 + (5)2 = (hypotenuse)2
1 + 25 = (hypotenuse)2
26 = (hypotenuse)2, so the hypotenuse = \(\sqrt{26}\).
Now, you can find sin C: \(\left ( \frac{opp}{hyp} \right )\)= \(\frac{1}{\sqrt{26}}\).
For all values, x, y, and z, if x ≤ y and y ≤ z, which of the following CANNOT be true?
I. x = z
II. x > z
III. x < z
-
Solution
You are given that x ≤ y and y ≤ z.
If x = y and y = z, then x = z could be true.
Eliminate answer choices F, J, and K, which show that Roman Numeral I (x = z) is NOT true.
If x < y and y < z, then x < z could be true. But x > z could not be true in either case.
So only II CANNOT be true, answer choice G.
Daniel is painting a wall in his bedroom. He can cover 36 square feet with 1 gallon of paint. If the wall is 8 feet high and 12 feet long, how many gallons, to the nearest whole gallon, will Daniel need to paint the wall?
-
Solution
You are given that 1 gallon of paint can cover 36 square feet.
The room is 8 feet by 12 feet, or 96 square feet. Set up a proportion:
\(\frac{1}{36}=\frac{x}{96}\)
Cross-multiply and solve for x:
36x = 96
x = approximately 2.666
The question asks you to round to the nearest whole gallon, so round up to 3 gallons.
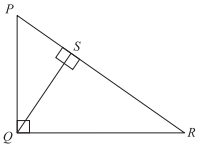
In the figure below, triangles PQR, PSQ, and QSR are right triangles. If the measure of angle P is 55°, what is the measure of angle R?
-
Solution
You are given that angle P is 55°.
Since PQR is a right triangle, angle Q is 90°.
So, angle R must be 180° − (55° + 90°) or 35°.
If x = 3 is 1 solution for the equation 2x2 −5x −a = 0, what is the value of a?
-
Solution
You are given that x = 3 is one solution, which means that (x − 3) is one of the factors of 2x2−5x−a = 0.
Since the coefficient of the x2–term is 2, you can set up the other factors as follows:
(2x + )(x − 3)
The x terms must equal –5, so apply the FOIL method to find the missing term:
−6x + x = −5x
−6x + x = −5x; the missing term must be 1.
Use FOIL again to solve for a:
(2x + 1)(x − 3)
2x2 − 6x + x − 3
2x2 − 5x − 3
Thus, a = 3.
For all x ≠ −3,\(\frac{x^{2} − 6x + 9}{6x − 18}\)?
-
Solution
First, factor the numerator and denominator:
\(\frac{x^{2} − 6x + 9}{6x − 18}=\frac{(x − 3)(x − 3)}{6(x − 3)}\)
Next, cancel out an (x −3) from the numerator and denominator, which leaves you with \(\frac{(x − 3)}{6}\).
For all x, x2 − (3x − 2) + 2x(4x − 1) = ?
-
Solution
To solve this problem, combine like terms. Remember to keep track of the negative signs!
x2 − (3x − 2) + 2x(4x − 1)
x2 − 3x + 2 + 8x2 − 2x
9x2 − 5x + 2