A total of f men went on a fishing trip. Each of the r boats that were used to carry the fishermen could accommodate a maximum number of m passengers. If one boat had 5 open spots and the remaining boats were filled to capacity, which of the following expresses the relationship among f , r, and m?
-
Solution
If each of the r boats that were used to carry the fishermen could accommodate a maximum number of m passengers, the total capacity of fisherman is rm.
Since only one boat had 5 open spots and the remaining boats were filled to capacity, the number of fishermen was 5 less than the total capacity, or rm − 5. Thus f = rm − 5.
If cos x = 5⁄7 and tan x = 4⁄5, what is sin x?
-
Solution
The cosine of any acute angle is the length of the adjacent side divided by the hypotenuse \(\left ( \frac{adj}{hyp} \right )\).
The tangent of any acute angle is the length of the opposite side divided by the length of the adjacent side \(\left ( \frac{opp}{adj} \right )\).
The sine of any acute angle is the length of the opposite side divided by the hypotenuse.
You are given that cos x = 5⁄7\(\left (\frac{adj}{hyp} \right )\) and tan x = 4⁄5\(\left (\frac{opp}{adj} \right )\).
Sin x must equal 4⁄7 \(\left (\frac{opp}{hyp} \right )\).
Given the graph below in the standard (x,y) coordinate plane, the slope of line a is ma and the slope of line b is mb. Which of the following statements about the slope of lines a and b is true?

-
Solution
Based on the figure, line a and line b are perpendicular lines, because they intersect to form right angles.
Perpendicular lines have slopes that are negative reciprocals. In other words, if the slope of line a is ma, the slope of line b is −1⁄ma.
You are given that the slope of line b is mb,so mb = −1⁄ma.
This is equivalent to ma = −1⁄mb.
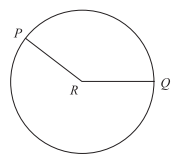
In the figure below, P and Q lie on the circle R, which has a radius of 9. If the angle PRQ is 120◦, what is the area of sector PRQ?
-
Solution
There are 360◦ in a circle.
∠PRQ is 120◦, so the sector makes up 120◦÷360◦, or 1⁄3, of the area of the circle.
To answer this question, determine the area of the entire circle and take 1⁄3 of the result to find the area of the sector.
The formula for the area of a circle is A = πr2.
The radius, 9, is given in the problem, so plug 9 into the formula:
= π(9)2
= 81π
You know that the sector is 1⁄3 of the circle, so divide the area of the entire circle by 3:
81π ÷ 3 = 27π
Which of the following intervals contains the solution to the equation x − 2 =\(\frac{2x + 5}{3}\)?
-
Solution
First, solve the equation for x:
x − 2 = \(\frac{2x + 5}{3}\)
3x − 6 = 2x + 5
x = 11
Only the interval 11 ≤ x<15 contains 11, so answer choice G must be correct.
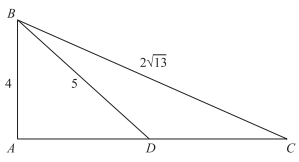
In the figure below, the lengths of the sides of triangle BAC are as shown. \(\overline{BD}\) bisects side \(\overline{AC}\). What is the length of DC?
-
Solution
The first step in answering this question is to use the Pythagorean Theorem,a2 + b2 = c2, to determine the length of AB.
BD, the line that bisects AC, creates a second triangle, BAD. Use the length of lines BD and AD to determine the length of AD (let AD = a).
a2 + 42 = 52
a2 + 16 = 25
a2 = 9
a = 3
Because you known that BD bisects AC, you know that the length of DC must also equal 3.
What values of x make the inequality −5x − 7 > 3x + 1 true?
-
Solution
The first step in answering this question is to rearrange the terms so that the x’s are all on one side of the inequality,
−5x − 7 > 3x + 1:
−7 > 8x + 1
The next step is to get x alone:
−8 > 8x
−1 > x, which is equivalent to x < −1.
José is building a scale model of a sailboat, complete with a main sail. The actual sailboat’s main sail measures 56 feet high with a base of 32 feet. If the model sailboat’s main sail has a base of 8 inches, how tall will the model’s main sail be, in inches?
-
Solution

A line in the standard (x,y) coordinate plane has a slope of 2⁄3 and passes through points (3,4) and (t,−2). What is the value of t?
-
Solution

In the figure below, PQRS is a rectangle with sides of lengths shown. X is the midpoint of \(\overline{SR}\). What is the perimeter of triangle PXQ?

-
Solution
You know that QRX is a right triangle, and QR = 4.
Since X is the midpoint of SR, which is 8, RX must equal 4.
QX = 4√2, since RX is an isosceles triangle where the hypotenuse is √2 times the measure of the legs of the triangle.
Since QX = 4√2, PX must also equal 4√2.
So, the perimeter of triangle PXQ is 8 + 4√2 + 4√2, or 8√2 + 8.

