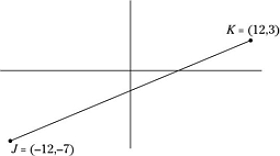
In the following figure, what is the length of \(\overline{JK}\) ?
-
Solution
Plug the values (–12, –7) and (12, 3) into the distance formula:
\(Distance = \sqrt{\left (x_{2} - x_{1} \right )^{2} + \left (y_{2} - y_{1} \right )^{2}}\) = \(\sqrt{\left (12 - \left (-12 \right ) \right )^{2} + \left (3 - \left (-7 \right ) \right )^{2}}\)
Now simplify to get the answer:
\(= \sqrt{\left (24 \right )^{2} + \left (10 \right )^{2}} = \sqrt{576 + 100} = \sqrt{676} = 26\)
What is the determinant of the matrix \(\begin{vmatrix} 3 & 6\\ -1 & 2 \end{vmatrix}\)?
-
Solution
The determinant of a matrix is a number, not a matrix, so rule out Choices (H), (J), and (K).
To determine which of the remaining answers is correct, use the determinant formula ad – bc:
(3 × 2) – (–6 × 1)
Simplify:
= 6 – (–6) = 6 + 6 = 12
Which of the following points on the xy-graph is the x-intercept of the equation y = 2x – 8?
-
Solution
The x-intercept of a line is the point where it crosses the x-axis — that is, where y = 0 — so the second coordinate must equal 0.
Therefore, you can rule out Choices (A) and (B).
To choose correctly among the three remaining answers, substitute 0 for y in the equation and solve for x:
y = 2x – 8
0 = 2x – 8
8 = 2x
4 = x
Thus, the x-intercept is (4, 0).
Antoine bought a new electric guitar that cost $588.60 after 9% sales tax was added. What was the price of the guitar without tax?
-
Solution
Let x be the original price of the guitar before tax.
Antoine paid $588.60 with a 9% percent increase on top of the original price.
Therefore, Antoine paid 109% of the original price, so you can create this equation:
1.09x = 588.60
Solve for x:
\(x = \frac{588.60}{1.09} = 540\)
What is the area of ΔRST in the following figure?

-
Solution
To begin, note that ΔSUR is a right triangle with a leg the length of 9 and a hypotenuse the length of 15, so it’s a 9-12-15 version of a 3-4-5 triangle; therefore, SU = 12.
ΔTUS is a right triangle with a leg the length of 12 and a hypotenuse the length of 13, so it’s a 5-12-13 triangle; therefore, UT = 5.

So the base of ΔRST is 14, and its height is 12.
Plug these values into the formula for the area of a triangle to get your answer:
A = 1⁄2bh = 1⁄2(14)(12) = 84
Danielle’s phone plan charges her $30 per month for the first 200 minutes and then $0.10 per minute for each subsequent minute.
If Danielle paid exactly $100 last month, how many minutes did she use?
-
Solution
Use the function you found for Question 29:
f(x) = 0.1x + 10
Plug in 100 for x and solve for x:
100 = 0.1x + 10
90 = 0.1x
900 = x
Danielle’s phone plan charges her $30 per month for the first 200 minutes and then $0.10 per minute for each subsequent minute.
Which of the following functions takes an input of any whole number value of x ≥ 200 and outputs the value for f(x) as the amount of dollars Danielle would pay for x minutes of phone usage?
-
Solution
Danielle pays $0.10 per minute, so the function includes 0.1x.
However, she gets 200 minutes with her initial $30, so the input x needs to be changed to x– 200 to account for this.
Therefore, the function includes 0.1(x – 200).
Additionally, she’s charged $30, so the function is:
f(x) = 0.1(x – 200) + 30
Simplify by distributing and combining to get the final function:
f(x) = 0.1x – 20 + 30
f(x) = 0.1x + 10
Jane ran around the perimeter of a rectangular park at a constant rate of 10 feet per second. The park has an area of 67,500 square feet, and its length is exactly three times its width. For how many seconds did Jane run?
-
Solution
The area of the park is 67,500 square feet.
If you let w equal the width of the park, the length is 3w.
Plug these numbers into the area formula for a rectangle and solve for w:
A = lw
67,500 = (3w)(w)
67,500 = 3w2
22,500 = w2
150 = w
If the width is 150 feet, the length is 150 × 3 = 450 feet.
Plug these numbers into the formula for the perimeter of a rectangle:
P = 2l + 2w = 2(450) + 2(150) = 900 + 300 = 1,200
The perimeter of the park is 1,200 feet.
Jane ran at 10 feet per second, so she ran for 120 seconds (because 1,200 ÷ 10 = 120).
If pq = 3, then p3q4 + p4q5 =
-
Solution
To begin, notice that the first term of p3q4 + p4q5 contains (pq)3 multiplied by an extra q, and the second term contains (pq)4 multiplied by an extra q.
As a result, you can factor those values out of each respective term to simplify:
p3q4 + p4q5 = (pq)3q + (pq)4q
Now you can substitute 3 for pq and simplify:
= (3)3q + (3)4q
= 27q + 81q
= 108q
If tanθ = 4⁄3, then sinθ = ?
-
Solution
Remember that tanθ = O⁄A, So if tanθ = 4⁄3, the opposite and adjacent sides of the triangle are in a ratio of 4:3.
Thus, the triangle is a 3-4-5 triangle (you can verify this with the Pythagorean theorem), so you can make the following sketch:

Use this figure and the formula for the sine to answer the question:
sinθ = O⁄H = 4⁄5

