A password for a computer system requires exactly 6 characters. Each character can be either one of the 26 letters from A to Z or one of the ten digits from 0 to 9. The first character must be a letter and the last character must be a digit. How many different possible passwords are there?
-
Solution
The first character must be a letter, so 26 possibilities exist for this character.
The last (6th) character must be a digit, so 10 possibilities exist for this one.
The remaining four characters can be either a letter or a digit, so 36 possibilities exist for each of these.
The following chart organizes this information:
1st 2nd 3rd 4th 5th 6th
26 36 36 36 36 10
Multiply these results:
26 × 36 × 36 × 36 × 36 × 10 = 436,700,160
This result has 9 digits, so it’s between 108(100,000,000) and 109(1,000,000,000).
If \(\frac{a + b}{10} = \frac{a – 0.1b^{2}}{a – b}\), what is the value of a?
-
Solution
Cross-multiply to get the two fractions out of the equation:
\(\frac{a + b}{10} = \frac{a - 0.1b^{2}}{a - b}\)
(a + b)(a - b) = 10(a - 0.1b2)
FOIL the left side and distribute the right side:
a2 – b2 = 10a – b2
Add b2 to both sides of the equation, and then divide by a:
a2 = 10a
a = 10
Let f(x) = x2 + 10x + 2. If g(x) is a transformation that moves f(x) both one unit up and one unit to the right, then g(x) =
-
Solution
The function g(x) is the transformation that moves f(x) = x2 + 10x + 2 one unit up and one unit to the right.
To move one unit up, add 1 to the entire function. And to move one unit to the right, substitute x– 1 for x in the function. Thus
g(x) = f(x – 1) + 1
Thus, you need to substitute x – 1 for x throughout the f(x) and to add 1 to f(x):
g(x) = (x – 1)2 + 10(x – 1) + 2 + 1
Now simplify:
= (x – 1)(x – 1) + 10(x – 1) + 2 + 1
= x2 – 2x + 1 + 10x – 10 + 2 + 1
= x2 + 8x – 6
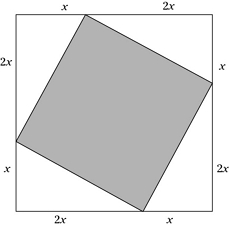
In the following figure, the area of the large square is 81. What is the area of the shaded square?
-
Solution
Each side of the large square has a length of x + 2x = 3x.
The area of the large square is 81, so each side of the square is √(81) = 9.
So one side of the square is 3x, which is equal to 9.
Thus:3x = 9
x = 3
So each triangle has legs of x = 3 and 2x = 6.
Plug these values into the Pythagorean theorem:
a2 + b2 = c2
32 + 62 = c2
Because c is the side of the shaded square, c2 is the area of this square.
So solve for c2:
9 + 36 = c2
45 = c2
Thus, the area of the shaded square is 45.
In the following figure, the area of the shaded region is 20% of the area of the whole circle centered at P.The angle shown measures d degrees. What is its measurement in radians?

-
Solution
The area of the shaded region is 20% of the whole circle, so d° is 20% of 360°:
d = (0.2)(360) = 72
Use the formula for converting degrees to radians, and plug in 72 for degrees and r for radians:
\(\frac{180}{\pi} = \frac{degrees}{radians}\)
\(\frac{180}{\pi} = \frac{72}{r}\)
Cross-multiply and solve for r:
180r = 72 π
\(r = \frac{72 \pi}{180}\)
r = 2⁄5 π
If 7x + 4y = 18 and 3x + y = –3, what is the value of x + y?
-
Solution
To solve, you want to multiply each equation by a number so that one of the two variables ends up with the same coefficient in both equations.
The easiest way to do so is to multiply every term in 3x + y = –3 by 4, and then subtract one equation from the other:
\(\frac{\begin{matrix} & 7x & + & 4y & = & 18\\ - & 12x & + & 4y & = & -12 \end{matrix}}{-5x \;\;\;\;\;\; = \;\;\;\;\; 30}\)
Next, solve for x:
–6 = x
Finally, plug –6 for x into one of the original equations and solve:
3x + y = –3
3(–6) + y = –3
–18 + y = –3
y = 15
Now you know that x + y = –6 + 15 = 9.
If you multiply a number by 3 and then add 40, the result is the same as if you first add 17 and then multiply by 2. What is the result if you subtract 9 from the number and then multiply by 4?
-
Solution
Let x be the number, and then translate the words into the following equation:
3x + 40 = 2(x + 17)
Simplify and solve for x:
3x + 40 = 2x + 34
x + 40 = 34
x = –6
If you subtract 9 from x and then multiply by 4, the result is:
4(–6 – 9) = 4(–15) = –60
Ansgar is writing a novel. He writes seven days a week. On each of those days he writes for at least 4 hours but never more than 8 hours. Last week, he wrote for exactly 46 hours. What is the maximum number of days on which he could have written for 8 hours?
-
Solution
Ansgar writes for at least 4 hours a day, so in 7 days he writes for at least 28 hours (because 4 × 7 = 28).
On any day that he wrote for 8 hours, he would have written for an additional 4 hours over the minimum.
Thus, the week he wrote 46 hours, he wrote for an extra 18 hours (because 46 – 28 = 18).
As a result, he could have written for an additional 4 hours on no more than 4 different days.
For example, here’s one possible schedule:
Day 1 Day 2 Day 3 Day 4 Day 5 Day 6 Day 7 Total
8 8 8 8 6 4 4 46
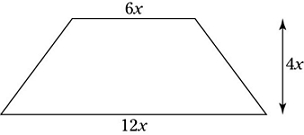
In the following figure, if the dimensions of the trapezoid are as shown and the area of the trapezoid is 144, what is the value of x?
-
Solution
Begin by plugging the height and the two bases into the formula for the area of a trapezoid:
\(Area = \frac{b_{1} + b_{2}}{2}h\)
\(144 = \frac{6x + 12x}{2}\left (4x \right )\)
\(144 = \frac{18x}{2}\left (4x \right )\)
Continue simplifying and solve for x:
144 = 9x(4x)
144 = 36x2
4 = x2
2 = x
A 25-foot ladder stands against a vertical wall at an angle of n degrees with the ground. If sin n = 4⁄5, how far is the base of the ladder from the wall?
-
Solution
Begin by drawing a picture of the ladder and wall:

Note that the question asks you to find the distance from the base of the ladder to the wall, which is the adjacent side of this triangle.
Begin by using the sine of n,which is the ratio of the opposite side over the hypotenuse:
sin n = O⁄H = 4⁄5
The hypotenuse is 25, so you can set up a proportion to find the length of the opposite side:
O⁄25 = 4⁄5
O × 5 = 100
O = 20
Now use the Pythagorean theorem to find the length of the adjacent side:
202 + b2 = 252
400 + b2 = 625
b2 = 225
b = 15
