If the triangle formed by lines AB, CD, and GH is an isosceles right triangle, angle 8 is greater than angle 7, and angle 8 is congruent to angle 5, which of the following is NOT true?
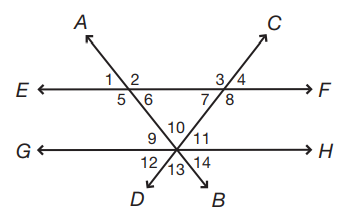
Lines EF and GH are parallel. The diagram is not to scale, and every angle is greater than 0°.
-
Solution
If angle 8 is greater than angle 7, angle 7 cannot be the right angle of the triangle; otherwise, angles 8 and 7 would be congruent. Therefore, angle 7 is one of the acute, congruent angles of the right triangle, which means that it measures 45°. Since angles 8 and 5 are congruent, angle 6 must be the other 45° angle of the triangle, making angle 10 the right angle of the triangle. Since angle 6 is 45° and angles 2 and 6 are supplementary, the measure of angle 2 is 180 – 45 = 135°. Since angles 6 and 9 are alternating angles, the measure of angle 9 is 45°, and since angles 7 and 12 are alternating angles, the measure of angle 12 is also 45°. Therefore, the sum of angles 9 and 12 is 45 + 45 = 90, not 135, so angle 2 is not equal to angle 9 + angle 12.
The measure of angle 11 is twice the measure of angle 14, and the measure of angle 8 is 2.5 times the measure of angle 14. What is the measure of angle 10?

Lines EF and GH are parallel. The diagram is not to scale, and every angle is greater than 0°.
-
Solution
If the measure of angle 14 is x,then the measure of angle 11 is 2x and the measure of angle 8 is 2.5x. Since angles 8 and 11 are supplementary, 2x + 2.5x = 180, 4.5x = 180, x = 40. Therefore, angle 14 = 40° and angle 11 = 2(40) = 80°. Since angles 10, 11, and 14 form a line, the measure of angle 10 is equal to 180 – (40 + 80) = 180 – 120 = 60°.
The measure of angle 5 is 10x + 2, the measure of angle 11 is 4x – 4, and the measure of angle 13 is 7x – 6. What is the sum of angles 10 and 7?

Lines EF and GH are parallel. The diagram is not to scale, and every angle is greater than 0°.
-
Solution
Angles 10 and 13 are vertical angles; their measures are equal. Angle 5 and the sum of angles 10 and 11 are equal, since angle 5 and the combination of angles 10 and 11 are alternating angles. Therefore, 10x + 2 = 4x – 4 + 7x – 6, 10x + 2 = 11x – 10, x = 12. Since the measure of an exterior angle is equal to the sum of the interior angles to which the exterior angle is not adjacent, angle 5 is equal to the sum of angles 10 and 7: 10(12) + 2 = 120 + 2 = 122°.
If angle 3 measures 10x + 15, angle 10 measures 8x – 3, and angle 6 measures 3x + 7, what is the measure of angle 7?

Lines EF and GH are parallel. The diagram is not to scale, and every angle is greater than 0°.
-
Solution
The measure of an exterior angle is equal to the sum of the interior angles to which the exterior angle is not adjacent. Therefore, angle 3 is equal to the sum of angles 6 and 10: 10x + 15 = 8x – 3 + 3x + 7, 10x + 15 = 11x + 4, x = 11. The measure of angle 3 is 10(11) + 15 = 110 + 15 = 125. Since angles 3 and 7 are supplementary, the measure of angle 7 is 180 – 125 = 55°.
If angles 6 and 7 are congruent, and the measure of angle 13 is 94°, what is the measure of angle 8?

Lines EF and GH are parallel. The diagram is not to scale, and every angle is greater than 0°.
-
Solution
Angles 10 and 13 are vertical angles. Since vertical angles are equal, angle 10 is also 94°. There are 180° in a triangle, and angles 6 and 7 are congruent. Therefore, 94 + x + x = 180, 2x = 86, x = 43. Since the measure of angle 7 is 43 and angles 7 and 8 are supplementary, the measure of angle 8 is equal to 180 – 43 = 137°.
Triangles GHI and PQR are similar and isosceles. If side HG of triangle GHI is congruent to side PQ, its corresponding side in triangle PQR, which of the following must be true?
-
Solution
Since the triangles are similar, the measures of their corresponding sides are in the same ratio.Sides HG and PQ are corresponding sides that are congruent. Therefore, the ratio of side HG to side PQ is 1:1. Each side of triangle GHI is congruent to its corresponding side; therefore, side GI is congruent to its corresponding side.
Triangles JKL and MNO are congruent and equilateral. If side JK measures 6x + 3 and side MN measures x2 – 4, what is the length of side NO?
-
Solution
Since triangles JKL and MNO are congruent and equilateral, every side of triangle JKL is congruent every other side of triangle JKL and congruent to every side of triangle MNO. Therefore, 6x + 3 = x2 – 4, x2 – 6x – 7, (x – 7)(x + 1) = 0, x = 7. Disregard the negative value of x, since a side of a triangle cannot be negative. Every length of triangles JKL and MNO is equal to 6(7) + 3 = 42 + 3 = 45.
If the length of \(\overline{BC}\) is x and the length of \(\overline{EF}\) is 1⁄5x, which of the following is NOT true?
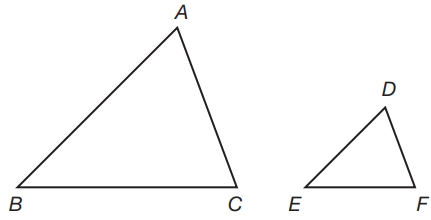
Triangles ABC and DEF are similar. The diagram is not to scale, and every angle is greater than 0°.
-
Solution
The measures of corresponding sides of similar triangles are in the same ratio. The ratio of side BC to side EF is 1: 1⁄5, or 5:1. Therefore, each side of triangle ABC is five times the length of its corresponding side in triangle DEF, and each side of triangle DEF is 1⁄5 the length of its corresponding side in triangle ABC. Corresponding angles of similar triangles are congruent. Therefore, angle A is congruent to angle D, not five times its measure.
Every side of triangle DEF is greater than 3. If the length of \(\overline{AB}\) is 10x – 2, the length of \(\overline{AB}\) is 6x, the length of \(\overline{AB}\) is 2x + 2, and the length of \(\overline{DF}\) is x + 2, what is the length of \(\overline{DF}\)?

Triangles ABC and DEF are similar. The diagram is not to scale, and every angle is greater than 0°.
-
Solution
The measures of corresponding sides of similar triangles are in the same ratio. The ratio of side AB to side DE is equal to the ratio of side AC to side DF. Therefore,\(\frac{10x-2}{2x-2}=\frac{5x}{x+2}\), (10x – 2)(x + 2) = (6x)(2x + 2), 10x2 – 2x + 20x – 4 = 12x2 + 12x, 2x2 – 6x + 4 = 0, x2 – 3x + 2 = 0, (x – 2)(x – 1) = 0, x = 1; x = 2. If x = 1, then side DF = (1) + 2 = 3. However, every side of triangle DEF is greater than 3. Therefore, x must be equal to 2; 2 + 2 = 4. The length of side DF is 4.
If the length of \(\overline{AB}\) is 90, the length of \(\overline{AB}\) is 60, and the length of \(\overline{AC}\) is 72, what is the length of \(\overline{AC}\)?

Triangles ABC and DEF are similar. The diagram is not to scale, and every angle is greater than 0°.
-
Solution
The measures of corresponding sides of similar triangles are in the same ratio. The ratio of side AB to side DE is equal to the ratio of side AC to side DF. Therefore, 9\(\frac{90}{60}=\frac{72}{x},\frac{3}{2}=\frac{72}{x},3x = 144,x = 48.\). The length of \(\overline{DF}\) is 48.