If – 6 < – 4r + 10 ≤ 2, what is the least possible value of 4r + 3 ?
-
Solution
Notice that this question is asking for an expression instead of a variable, so manipulate the inequality to so that you get 4r + 3 in the inequality.
Treat each side of the inequality separately to avoid confusion.
Starting with the -6 < -4r + 10 part, multiply both sides of the inequality by -1, remembering to switch the sign, to get 6 > 4r - 10.
Add 13 to each side to get 19 > 4r + 3. Then solve the right side of the inequality.
Again, multiply both sides of the inequality by -1, switching the sign to get 4r - 10 ≥ -2.
Now add 13 to each side of the equation: 4r + 3 ≥ 11.
Finally, combine the equations to get the range for 4r + 3.
Since the question asks for the least possible value of the expression, 11, (D), is the correct answer to the question.
If you see the answer before the last step above, you don't need to combine the equations.
If the product of x and y is 76, and x is twice the square of y, which of the following pairs of equations could be used to determine the values of x and y ?
-
Solution
Translate each statement, piece by piece.
The first part tells us that "the product of x and y is 76." Since product means multiplication, the first equation must be xy = 76, so you can eliminate (C).
The second part says that "x is twice the square of y," which translates to x = 2y2, so eliminate (B) and (D), and (A) is the only choice left.
Notice that only the y needs to be squared, which is why (B) is wrong.
The second equation for (B) would be written as "the square of twice y," which is not what the problem stated.
If \(\frac{2x}{x^{2} + 1} = \frac{2}{x + 2}\), what is the value of x ?
-
Solution
To solve this equation, use cross multiplication to get (2x)(x + 2) = (x2 + 1)(2).
Expand the equation to get 2x2 + 4x = 2x2 + 2.
Once you combine like terms, the result is 2x2 - 2x2 + 4x = 2 or 4x = 2.
Solve for x by dividing both sides by 4 to get x = 1⁄2, which is (B).
If x + 6 > 0 and 1 – 2x > -1, then x could equal each of the following EXCEPT
-
Solution
Solve the first inequality by subtracting 6 from each side so that x > -6.
You are looking for values that won't work for x, and x cannot equal -6.
Therefore, the answer must be (A).
Just to be sure, solve the next inequality by subtracting 1 from each side to get -2x > -2.
Divide by -2, remembering to switch the sign because you are dividing by a negative number, to get x < 1.
The values in (B), (C), and (D) fit this requirement as well, so they are values for x and not the correct answer.
If 4x · n2 = 4x + 1 · n and x and n are both positive integers, what is the value of n ?
-
Solution
First simplify the equation 4x · n2 = 4x + 1 • n to 4x • n = 4x + 1, and then try an easy number for x.
f x = 2, then 42 • n = 42 + 1.
Since 16n2 = 43, then 16n2 = 64 and n2 = 4.
So n = 2 The correct answer is (A).
If each number in the following sum were increased by t, the new sum would be 4.22. What is the value of t ?
\(\frac{\begin{matrix} & 0.65\\ & 0.85\\ & 0.38\\ + & 0.86 \end{matrix}}{\;\;\;\;\;\;2.74}\)-
Solution
To figure out how much you need to add to 2.74 to get to 4.22, take 4.22 − 2.74 on your calculator.
The difference between the two numbers is 1.48.
This increase reflects the same number, t, added to each of the four numbers on the list.
Divide 1.48 by 4 to find that t = 0.37, which is (D).
If √x + 22 = 38, what is the value of x ?
-
Solution
To solve this equation, get √x by itself. √x = 16, so square both sides: (√x)2 = 162, so x = 256. Choice (D) is correct.
Which of the following graphs shows a strong positive association between x and y ?
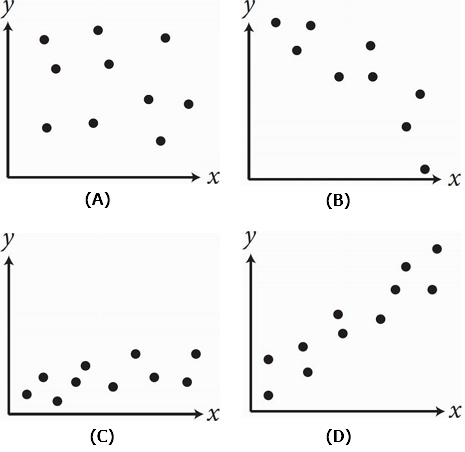
-
Solution
A “strong positive association” means that as one variable increases, the other one increases.
This will be shown as a line that angles through the graph from the lower left to the upper right.
These scatterplots don’t have any lines of best fit drawn on them, so imagine the line that would go through most of the points on each graph.
In (A), the points are all over the place, so no line of best fit can even be drawn.
Eliminate (A).
In (B), the line that hits most of the points would go from the upper left to the lower right.
This is a negative association, not a positive one, so eliminate (B).
In (C), the line would go straight across, parallel to the x-axis.
This is not a positive association, so eliminate (C).
The correct answer is (D).
If 3x = 12, what is the value of \(\frac{24}{x}\)
-
Solution
First, solve for x. Divide both sides of the equation by 3, and you get x = 4.
Then divide 24 by 4, which gives you 6, which is (D).
If 7 times a number is 84, what is 4 times the number?
-
Solution
Translate the words into math: 7 × n = 84, and we want to know the value of 4n.
7n = 84, so n = 12, and 4n = 48, (C).