As part of a recent wildlife conservation effort in Guatemala, park rangers in Tikal National Park have tracked the growing number of white-nosed coati living within a certain protected region over the period 1994-2004.

According to the data above, if the population of coati in the protected region of Tikal National Park increased at the same rate from 2004-2006 as it did from 2000-2004, then what was the number of coati in the park in 2006 ?

A. 180
B. 190
C. 200
D. 210

Solution

You can see from the graph that from 2000 to 2002, the number of coati increased from 140 to 160.

From 2002 to 2004, the number increased from 160 to 180.

Therefore, the number of coati is increasing at a rate of 20 every 2 years.

In 2006, if the rate of increase remains the same, the number of coati should be 180 + 20 = 200, which is (C).

Fuel Efficiency by Vehicle Weight

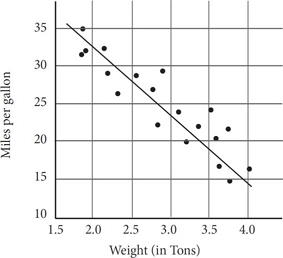
The scatterplot above shows the fuel efficiency, in miles per gallon, of a variety of vehicles weighing between 1.5 and 4 tons. Based on the line of best fit to the data represented, which of the following is the closest to the expected miles per gallon of a vehicle that weighs 3 tons?

A. 20
B. 24
C. 27
D. 28

Solution

Weight is shown on the horizontal axis of the graph, given in tons.

Look for the mark indicating 3 on this axis; then draw a vertical line from that mark to the line of best fit.

Once you hit it, draw a horizontal line over to the vertical axis.

It should hit between 20 and 25 miles per gallon, slightly closer to the mark for 25.

This makes (B) the credited response.

Draw your lines carefully, using your answer sheet as a straightedge if necessary, to avoid trap answers like the close-but-not-quite (C).

A developer is creating a plan for a 44-acre park that includes a 4-acre lake that cannot be developed. If 8 to 10 acres, inclusive, must be reserved for soccer fields, which of the following inequalities shows all possible values for p, the amount of land that within the park that is available for development?

A. 26 ≤ p ≤ 40
B. 30 ≤ p ≤ 32
C. 34 ≤ p ≤ 36
D. 36 ≤ p ≤ 40

Solution

In order to find the undeveloped area, take the entire area of the park and subtract the area of the developed portions.

Subtract the 4 acre lake to get 44 - 4 = 40 undeveloped acres.

Next, subtract the largest and smallest possible soccer field area: 40 - 10 = 30, and 40 - 8 = 32.

Therefore, the correct answer is (B).

Taylor is 6 feet tall. If 1 foot is equal to approximately 0.3 meters, then which of the following is closest to Taylor’s height in meters?

A. 1.8
B. 2
C. 18
D. 20

Solution

Set up a proportion: $\frac{1 \;\; foot}{0.30 \;\; meters} = \frac{6 \;\; feet}{x \;\; meters}$.

Cross-multiply to get x = 6 × 0.30 = 1.8 meters.

Therefore, the correct answer is (A).

An air pump at a gas station dispenses 90 pounds of air for $0.25. Which of the following expressions gives the number of pounds of air dispensed, P, for d dollars?

A. P = d + 90
B. P = d + 360
C. P = 90d
D. P = 360d

Solution

Whenever there are variables in the question and in the answers, think Plugging In.

Let d = 2. For $1 the air pump dispenses 90 × 4 = 360 pounds of air.

Therefore, for $2 the air pump will dispense 360 × 2 = 720 pounds of air.

Plug in 2 for d in the answer choices to see which answer equals 720.

Choice (A) becomes P = 2 + 90 = 92.

Eliminate (A).

Choice (B) becomes P = 2 + 360 = 362.

Eliminate (B). Choice (C) becomes P = 90(2) = 180.

Eliminate (C).

Choice (D) becomes P = 360(2) = 720.

Therefore, the correct answer is (D).

Mr. Lastorka’s science class is running experiments with an energy-efficient model electric car. As the initial rate of energy delivered to the car, measured in watts, increases, the number of millimeters moved by the car from its starting position increases exponentially. The results of several trial runs are shown on the scatterplot graph below.

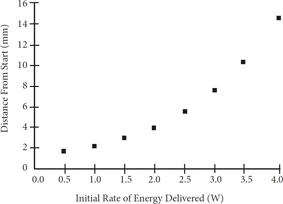
Based on the data, the students in Mr. Lastorka’s class determine the exact equation involving Watts, x, and total distance from start, y . They call the function y = f(x). Mr. Lastorka then instructs his class to reflect y = f(x) over the x-axis. He challenges each student to determine the new function and what it would mean from a physics perspective. Four student pairs gave their answers below. Who is correct, and for what reasons?

A. Charles and Shannon, who identify the new equation as y = -2x and explain that the new graph indicates that the car is still moving forward at the same rate as before.
B. Michael and Lauren, who identify the new equation as y = -2x and explain that the new graph indicates the car is now moving in reverse at the same rate as before.
C. Matthew and Karen, who identify the new equation as y = 2-x and explain that the new graph indicates that the car is now moving forward more rapidly than before.
D. Andy and Joanie, who identify the new equation as y = 2-x and explain that the new graph indicates that the car is no longer moving in any direction.

Solution

If the original graph is reflected across the x-axis, the x-values will remain the same but the y-values will switch signs.

Since the y-axis represents distance from start, negative y-values means that the car is now going in reverse.

The only answer that matches this information is (B).

Medical residents at Lakewood Hospital are choosing their individual specialties. Among them, 40% choose cardiology, 16% choose oncology, 34% choose endocrinology, and the remaining x% choose hematology. Once the doctors pick their first specialty, they are then each asked to choose a second specialty from the previous four options in case their original specialty is already filled. They may not pick their original specialty again. 20% of those who originally picked cardiology choose oncology as their second choice. If no other field chooses oncology as their second choice, and the hospital boasts 200 medical residents, then what is the total number of residents who named oncology as either their first or second choice, in terms of x ?

A. 8x - 128
B. 8x - 144
C. x² + 24x - 188
D. x² - 24x + 188

Solution

16% of the 200 medical residents named oncology as their first choice: $\frac{16}{100}$(200) or (0.16)(200) = 32 residents.

40% of the 200 medical residents named cardiology as their first choice: $\frac{40}{100}$(200) or (0.4)(200) = 80 residents.

Of these 80 residents, 20% chose oncology as their second choice: $\frac{20}{100}$(80) or (0.2)(80) = 16 residents.

The total number of residents who named oncology as either their first or second choice was therefore 32 + 16 = 48 residents.

To find the value of x, you need to subtract the percentages given in the question from the total, 100%: 100 - 40 - 16 - 34 = x = 10%.

Now, plug x = 10 into the answer choices in order to determine which one matches your target of 48 residents.

Only (D) works: x² - 24x + 188 = 100 - 24(10) + 188 = 100 - 240 + 188 = 48.

Circle O (not shown) is divided into three sectors. Points P, Q, and R are on the circumference of the circle. Sector POR has an area of 8π, and sector ROQ has an area of 6π. If the radius of circle O is 4, what is the measure of the central angle of sector QOP, in degrees?

A. 45
B. 90
C. 135
D. 180

Solution

Since the radius of the circle is 4, the area of the entire circle is πr² = π(4²) = 16π.

Sector POR has an area of 8π and sector ROQ has an area of 6π, so the remaining sector (QOP) has an area of 16π - 8π - 6π = 2π.

You can set up a proportion to determine the associated angle using the following formula: $\frac{sector \;\; area}{total \;\; area} = \frac{sector \;\; angle}{360^{\circ}}$.

Using the numbers you now have, your calculation will look like this: $\frac{2 \pi}{16 \pi} = \frac{sector \;\; angle}{360^{\circ}} \;\; or \;\; \frac{1}{8} = \frac{sector \;\; angle}{360^{\circ}}$.

Multiply both sides of the equation by 360 to determine that the sector angle is 45°, which is (A).

A certain polynomial, P, has a degree of 2. Polynomial P has zeros of 2 and -3, and a > 0 when the function of polynomial P is written in the form of y = ax2 + bx + c. Given this information, which of the following could be the graph of polynomial P ?

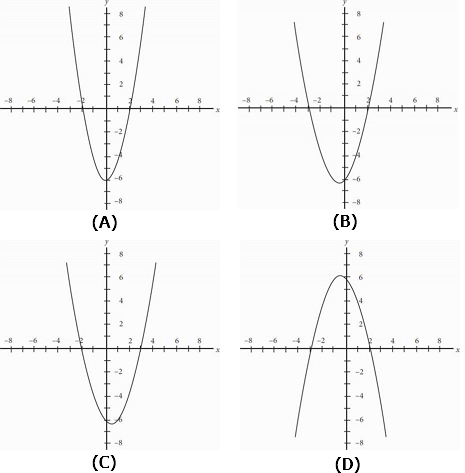
Solution

The best way to deal with this question is through POE.

If the polynomial has zeroes of 2 and -3, then that means you have two points: (2,0) and (-3,0)-eliminate (A) and (C).

Since it is given in the question that a > 0 when the parabola is in the form y = ax² + bx + c, the parabola must be pointed upwards-eliminate (D) and choose (B).

A professional baseball team wishes to average 45,500 ticket purchases per game for the entire 162-game season. Through the first 60 games of the season, the team has averaged 43,000 ticket purchases per game. Which of the following most closely approximates how many ticket purchases per game the team must average for the remainder of the season in order to hit its overall goal of an average of 45,500 ticket purchases per game for the season?

A. 46970
B. 47880
C. 48000
D. 48220

Solution

There are 162 games in the season, so the team needs a total of 162 × 45,500 = 7,371,000 ticket purchases to have a mean of 45,500 ticket purchases per game for the season.

The 60 games with an average total ticket purchase of 43,000 gives a total of 2,580,000 ticket purchases, leaving 4,791,000 ticket purchases left for the team to reach its goal.

Dividing 4,791,000 by 102 makes (A) the closest value to the average of 46,971 ticket purchases per game the team needs to make.

UnAttempted

0

Attempted

0

Correct

0

Wrong

0

Complete