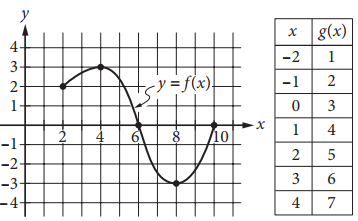
The complete graph of the function f and a table of values for the function g are shown above. The maximum value of f is k. What is the value of g(k) ?
-
Solution
The maximum value of the function f occurs at the highest point on the graph of y = f(x); the highest point on the graph is (4, 3). For any point on the graph of f, the y-coordinate gives the value of the function at the x-coordinate; therefore, the maximum value of the function f is 3. It is stated that k is the maximum value of f, so k = 3. Thus, g (k) = g (3). From the table of values for g, it can be seen that when x = 3, g (3) = 6.
Choice A is incorrect and may result from using the x-coordinate of the maximum point as the value of k. Choice C is incorrect; it is the value of k, not of g (k). Choice D is incorrect and may be the result of giving the value of x that makes g (x) = 3 instead of finding the value of g (x) when x = 3.
A photocopy machine is initially loaded with 5,000 sheets of paper. The machine starts a large job and copies at a constant rate. After 20 minutes, it has used 30% of the paper. Which of the following equations models the number of sheets of paper, p, remaining in the machine m minutes after the machine started printing?
-
Solution
Since the machine copies at a constant rate, the relationship between p, the number of sheets of paper remaining, and m, the time in minutes since the machine started printing, is modeled by a linear equation. The initial number of sheets of paper is given as 5,000. It is also given that the machine used 30% of those 5,000 sheets in 20 minutes, so it used 0.30 × 5,000 = 1,500 sheets in 20 minutes. Therefore, the number of sheets used per minute is \(\frac{1,500}{20}\) = 75. To determine the number of sheets of paper used m minutes after the machine started printing, multiply 75 by m, which gives 75m. Therefore, a linear equation modeling this relationship is the number of sheets remaining equals the initial number of sheets of paper minus the number of sheets of paper used m minutes after the machine started printing, which is p = 5,000 − 75m.
Choice A is incorrect and may be the result of using the given number of minutes, 20, as the rate at which the copy machine uses paper. However, the rate is 75, not 20, sheets per minute. Choices C and D are incorrect because they aren’t linear equations; they assume that the copy machine prints at a nonconstant rate.
The 22 students in a health class conducted an experiment in which they each recorded their pulse rates, in beats per minute, before and after completing a light exercise routine. The dot plots below display the results.

Let s1 and r1 be the standard deviation and range, respectively, of the data before exercise, and let s2 and r2 be the standard deviation and range, respectively, of the data after exercise. Which of the following is true?
-
Solution
The two data sets have the same range. The first data set has a range of 88 − 56 = 32, and the second data set has a range of 112 − 80 = 32. Alternatively, it can be seen visually that the ranges are the same because the two dot plots are aligned, the scales of the graphs are the same, and the graphs have the same width. The two data sets have different standard deviations. Both dot plots show distributions that have a mean near the center value of the dot plot. The first dot plot shows most values clustered near the mean, while the second dot plot shows most values farther from the mean. Therefore, the standard deviations of the two data sets are not equal—the data represented by the second dot plot has a greater standard deviation.
Choices A, B, and C are incorrect because they incorrectly assert either that the standard deviations are the same or that the ranges are different.
In the xy-plane, the point (p,r) lies on the line with equation y = x + b, where b is a constant. The point with coordinates (2p,5r) lies on the line with equation y = 2x + b. If p ≠ 0, what is the value of r⁄2p?
-
Solution
Since the point (p, r) lies on the line with equation y = x + b, the point must satisfy the equation. Substituting p for x and r for y in the equation y = x + b gives r = p + b. Similarly, since the point (2p, 5r) lies on the line with the equation y = 2x + b, the point must satisfy the equation. Substituting 2p for x and 5r for y in the equation y = 2x + b gives 5r = 2(2p) + b, or 5r = 4p + b. Solving each equation for b gives b = r − p and b = 5r − 4p, respectively. Substituting r − p for b in the equation b = 5r − 4p gives r − p = 5r − 4p. Subtracting r from each side of the equation and adding 4p to each side of the equation gives 3p = 4r. Dividing each side of the equation by p and dividing each side of the equation by 4 gives 3⁄4 = r⁄p.
Choices A, C, and D are incorrect. Choices A and D may be the result of incorrectly forming the answer out of the coefficients in the point (2p, 5r). Choice C may be the result of confusing r and p.
To determine the mean number of children per household in a community, Tabitha surveyed 20 families at a playground. For the 20 families surveyed, the mean number of children per household was 2.4. Which of the following statements must be true?
-
Solution
In order to use a sample mean to estimate the mean for a population, the sample must be representative of the population (for example, a simple random sample). In this case, Tabitha surveyed 20 families in a playground. Families in the playground are more likely to have children than other households in the community. Therefore, the sample isn’t representative of the population. Hence, the sampling method is flawed and may produce a biased estimate.
Choices A and D are incorrect because they incorrectly assume the sampling method is unbiased. Choice B is incorrect because a sample of size 20 could be large enough to make an estimate if the sample had been representative of all the families in the community.
Population of Greenleaf, Idaho
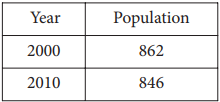
The table above shows the population of Greenleaf, Idaho, for the years 2000 and 2010. If the relationship between population and year is linear, which of the following functions P models the population of Greenleaf t years after 2000?
-
Solution
It is given that the relationship between population and year is linear; therefore, the function that models the population t years after 2000 is of the form P(t) = mt + b, where m is the slope and b is the population when t = 0. In the year 2000, t = 0. Therefore, b = 862. The slope is given by m =\(\frac{P(10) − P(0)}{10 − 0}=\frac{846 − 862}{10 − 0}=\frac{−16}{10}= −1.6\). Therefore, P(t) = −1.6t + 862,which is equivalent to the equation in choice A.
Choice B is incorrect and may be the result of incorrectly calculating the slope as just the change in the value of P. Choice C is incorrect and may be the result of the same error as in choice B, in addition to incorrectly using t to represent the year, instead of the number of years after 2000. Choice D is incorrect and may be the result of incorrectly using t to represent the year instead of the number of years after 2000.
For the finale of a TV show, viewers could use either social media or a text message to vote for their favorite of two contestants. The contestant receiving more than 50% of the vote won. An estimated 10% of the viewers voted, and 30% of the votes were cast on social media. Contestant 2 earned 70% of the votes cast using social media and 40% of the votes cast using a text message. Based on this information, which of the following is an accurate conclusion?
-
Solution
It is given that Contestant 2 earned 70% of the votes cast using social media and 40% of the votes cast using a text message. Based on this information, viewers voting by social media were more likely to prefer Contestant 2 than were viewers voting by text message.
Choices A, B, and C are incorrect. There is not enough information about the viewers to reach these conclusions.
M = 1,800(1.02)t
The equation above models the number of members, M, of a gym t years after the gym opens. Of the following, which equation models the number of members of the gym q quarter years after the gym opens?
-
Solution
In 1 year, there are 4 quarter years, so the number of quarter years, q, is 4 times the number of years, t; that is, q = 4t.
This is equivalent to t = q⁄4, and substituting this into the expression for M in terms of t gives M = 1,800(1.02)q⁄4.
Choices B and D are incorrect and may be the result of incorrectly using t = 4q. In choice D, 1.024q = 1.024(q), which is approximately 1.082q. Choice C is incorrect and may be the result of incorrectly using t = 4q and unnecessarily dividing 0.02 by 4.
Which of the following is closest to the percent increase in the billions of pounds of plastic produced in the United States from 2000 to 2003?
-
Solution
Since x is the number of years since 1985, the year 2000 corresponds to x = 15 and the year 2003 corresponds to x = 18. The corresponding points on the line of best fit are approximately (15, 98) and (18, 107). This means that approximately 98 billion pounds of plastic were produced in 2000 and approximately 107 billion pounds of plastic were produced in 2003. To calculate the percent increase, subtract the amount of plastic produced in 2000 from the amount of plastic produced in 2003 and then divide the result by the amount of plastic produced in 2000 and multiply by 100. This yields (\(\frac{107 − 98}{98}\)) ∙ 100 = 9.2, or approximately 10%.
Choices B and C are incorrect and may be the result of misreading the graph or making an arithmetic error. Choice D is incorrect and may be the result of approximating the amount of plastic produced, in billions of pounds, in the year 2003 (x = 18).
refer to the following information.
Between 1985 and 2003, data were collected every three years on the amount of plastic produced annually in the United States, in billions of pounds. The graph below shows the data and a line of best fit. The equation of the line of best fit is y = 3.39 + 46.89 x , where x is the number of years since 1985 and y is the amount of plastic produced annually, in billions of pounds.

Which of the following is the best interpretation of the number 3.39 in the context of the problem?
-
Solution
The number 3.39 in the equation y = 3.39x + 46.89 is the slope, which is the change in y per unit change in x. Because y represents the amount of plastic produced annually, in billions of pounds, and x represents the number of years since 1985, the number 3.39 represents the rate of change of the amount of plastic produced with respect to time, in units of billions of pounds per year. The change is an increase since 3.39 is positive, and it is described as an average change because the data show increases that are sometimes more and sometimes less than 3.39.
Choice A is incorrect. It is the interpretation of the number 46.89 in the line of best fit equation, y = 3.39x + 46.89. Choices B and C are incorrect because they are expressed in the wrong units. The number 3.39 has units of billions of pounds per year, but choice B has units of years and choice C has units of billions of pounds.