The score on a trivia game is obtained by subtracting the number of incorrect answers from twice the number of correct answers. If a player answered 40 questions and obtained a score of 50, how many questions did the player answer correctly?
-
Solution
The correct answer is 30. Let x represent the number of correct answers from the player and y represent the number of incorrect answers from the player. Since the player answered 40 questions in total, the equation x + y = 40 represents this situation. Also, since the score is found by subtracting the number of incorrect answers from twice the number of correct answers and the player received a score of 50, the equation 2x – y = 50 represents this situation. Adding the system of two equations together yields (x + y) + (2x – y) = 40 + 50. This can be rewritten as 3x = 90. Finally, solving for x by dividing both sides of the equation by 3 yields x = 30.
Line t is shown in the xy-plane below.

What is the slope of line t ?
-
Solution
The correct answer is 2⁄5. The slope of the line can be found by selecting any two points (x1, y1) and (x2, y2) on the line and then dividing the difference of the y-coordinates (y2 – y1) by the difference of the x-coordinates (x2 – x1). Using the points (−6, −\(\frac{27}{5}\)) and (9, 3⁄5), the slope is \(\frac{\frac{3}{5}-(-\frac{27}{5})}{9 – (–6)}=\frac{\frac{30}{5}}{15}\). This can be rewritten as \(\frac{6}{15}\), which reduces to 2⁄5. Any of the following equivalent expressions can be gridded as the correct answer: 2/5, .4, .40, .400, 4/10, 8/20.
In 1854, during the California gold rush, each ounce of gold was worth $20, and the largest known mass of gold found in California was worth $62,400 in that year. What was the weight, in pounds, of this mass of gold? (16 ounces = 1 pound)
-
Solution
The correct answer is 195. Since the mass of gold was worth $62,400 and each ounce of gold was worth $20, the mass of the gold was \(\frac{62,400}{20}\) = 3120 ounces. Since 1 pound = 16 ounces, 3120 ounces is equivalent to \(\frac{3120}{16}\)= 195 pounds.
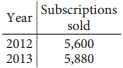
The manager of an online news service received the report above on the number of subscriptions sold by the service. The manager estimated that the percent increase from 2012 to 2013 would be double the percent increase from 2013 to 2014. How many subscriptions did the manager expect would be sold in 2014?
-
Solution
The percent increase from 2012 to 2013 was \(\frac{5,880 – 5,600}{5,600}\) = 0.05, or 5%. Since the percent increase from 2012 to 2013 was estimated to be double the percent increase from 2013 to 2014, the percent increase from 2013 to 2014 was expected to be 2.5%.Therefore, the number of subscriptions sold in 2014 is expected to be the number of subscriptions sold in 2013 multiplied by (1 + 0.025), or 5,880(1.025) = 6,027.
Choices A and C are incorrect and may be the result of a conceptual or calculation error. Choice D is incorrect and is the result of interpreting the percent increase from 2013 to 2014 as double the percent increase from 2012 to 2013.
A circle in the xy‑plane has equation (x + 3)2 + (y – 1)2 =25 Which of the following points does NOT lie in the interior of the circle?
-
Solution
The circle with equation (x + 3)2 + (y – 1)2 = 25 has center (–3, 1) and radius 5. For a point to be inside of the circle, the distance from that point to the center must be less than the radius, 5.The distance between (3, 2) and (–3, 1) is \(\sqrt{(−3 − 3)^{2} + (1 − 2)^{2}}=\sqrt{(-6)^{2}+(-1)^{2}}=\sqrt{37}\), which is greater than 5. Therefore, (3, 2) does NOT lie in the interior of the circle.
Choice A is incorrect. The distance between (–7, 3) and (–3, 1) is \(\sqrt{(−7 + 3)^{2}+ (3 − 1)^{2}}=\sqrt{(−4)^{2} + (2)^{2}}=\sqrt{20}\),which is less than 5,and therefore (–7, 3) lies in the interior of the circle. Choice B is incorrect because it is the center of the circle. Choice C is incorrect because the distance between (0, 0) and (–3, 1) is \(\sqrt{(0 + 3)^{2}+ (0 − 1)^{2}}=\sqrt{(3)^{2}+(1)^{2}}=\sqrt{8}\), which is less than 5, and therefore (0, 0) lies in the interior of the circle.

In the xy‑plane above, a point (not shown) with coordinates (s, t) lies on the graph of the linear function f. If s and t are positive integers, what is the ratio of t to s ?
-
Solution
The line shown has a slope of \(\frac{6 − 0}{3 − 0}=2\) and a y-intercept of (0, 0); therefore, the equation of the line is y = 2x. This means that for each point on the line, the value of the y-coordinate is twice the value of the x-coordinate. Therefore, for the point (s, t), the ratio of t to s is 2 to 1.
Choice A is incorrect and would be the ratio of t to s if the slope of the line were 1⁄3. Choice B is incorrect and would be the ratio of t to s if the slope of the line were 1⁄2. Choice D is incorrect and would be the ratio of t to s if the slope of the line were 3.
The world’s population has grown at an average rate of 1.9 percent per year since 1945. There were approximately 4 billion people in the world in 1975. Which of the following functions represents the world’s population P, in billions of people, t years since 1975 ? (1 billion = 1,000,000,000)
-
Solution
Because the world’s population has grown at an average rate of 1.9% per year since 1945, it follows that the world’s population has been growing by a constant factor of 1.019 since 1945.If the world’s population in 1975 was about 4 billion, in 1976 the world’s population would have been about 4(1.019); in 1977 the world’s population would have been about 4(1.019)(1.019), or 4(1.019)2; and so forth. Therefore, the world’s population, P(t), t years since 1975 could be represented by the function P(t) = 4(1.019)t.
Choice B is incorrect because it represents a 90% increase in population each year. Choices C and D are incorrect because they are linear models, which represent situations that have a constant growth.
If the 180 food calories in a granola bar come entirely from p grams of protein, f grams of fat, and c grams of carbohydrate, which of the following expresses f in terms of p and c ?
-
Solution
It is given that there are 4.0 food calories per gram of protein, 9.0 food calories per gram of fat, and 4.0 food calories per gram of carbohydrate. If 180 food calories in a granola bar came from p grams of protein, f grams of fat, and c grams of carbohydrate, then the situation can be represented by the equation 180 = 4p + 9f + 4c. The equation can then be rewritten in terms of f by subtracting 4p and 4c from both sides of the equation and then dividing both sides of the equation by 9. The result is the equation f = 20 − 4⁄9(p + c).
Choices A, C, and D are incorrect and may be the result of not representing the situation with the correct equation or incorrectly rewriting the equation in terms of f.
refer to the following information.
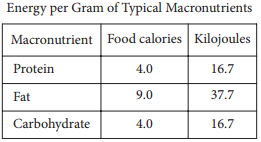
The table above gives the typical amounts of energy per gram, expressed in both food calories and kilojoules, of the three macronutrients in food.
If x food calories is equivalent to k kilojoules, of the following, which best represents the relationship between x and k ?
-
Solution
The relationship between x food calories and k kilojoules can be modeled as a proportional relationship. Let (x1, k1) and (x2, k2) represent the values in the first two rows in the table:(4.0, 16.7) and (9.0, 37.7). The rate of change, or \(\frac{(k_{2}-K_{1})}{(x_{2}-x_{1})}\), is \(\frac{21}{5}\) = 4.2;
therefore, the equation that best represents the relationship between x and k is k = 4.2x.
Choice A is incorrect and may be the result of calculating the rate of change using \(\frac{(x_{2}-x_{1})}{(k_{2}-K_{1})}\). Choice C is incorrect and may be the result of confusing the independent and dependent variables. Choice D is incorrect and may be the result of an error when setting up the equation.
h(t) = −16t2 + 10t + 72
The function above models the height h, in feet, of an object above ground t seconds after being launched straight up in the air. What does the number 72 represent in the function?
-
Solution
The variable t represents the seconds after the object is launched. Since h(0) = 72, this, means that the height, in feet, at 0 seconds, or the initial height, is 72 feet.
Choices B, C, and D are incorrect and may be the result of misinterpreting the function in context.