6 − 9 > 12 x y
Which of the following inequalities is equivalent to the inequality above?
-
Solution
Both sides of the given inequality can be divided by 3 to yield 2x − 3y > 4.
Choices A, C, and D are incorrect because they are not equivalent to (do not have the same solution set as) the given inequality. For example, the ordered pair (0, −1.5) is a solution to the given inequality, but it is not a solution to any of the inequalities in choices A, C, or D.
A website-hosting service charges businesses a onetime setup fee of $350 plus d dollars for each month. If a business owner paid $1,010 for the first 12 months, including the setup fee, what is the value of d ?
-
Solution
The equation 12d + 350 = 1,010 can be used to determine d, the number of dollars charged per month. Subtracting 350 from both sides of this equation yields 12d = 660, and then dividing both sides of the equation by 12 yields d = 55.
Choice A is incorrect. If d were equal to 25, the first 12 months would cost 350 + (12)(25) = 650 dollars, not $1,010. Choice B is incorrect. If d were equal to 35, the first 12 months would cost 350 + (12)(35) = 770 dollars, not $1,010. Choice C is incorrect. If d were equal to 45, the first 12 months would cost 350 + (12)(45) = 890 dollars, not $1,010.
Snow fell and then stopped for a time. When the snow began to fall again, it fell at a faster rate than it had initially. Assuming that none of the snow melted during the time indicated, which of the following graphs could model the total accumulation of snow versus time?
-
Solution
The leftmost segment in choice A, which represents the first time period,shows that the snow accumulated at a certain rate; the middle segment, which represents the second time period, is horizontal, showing that the snow stopped accumulating; and the rightmost segment, which represents the third time period, is steeper than the first segment, indicating that the snow accumulated at a faster rate than it did during the first time period.
Choice B is incorrect. This graph shows snow accumulating faster during the first time period than during the third time period; however, the question says that the rate of snow accumulation in the third time period is higher than in the first time period. Choice C is incorrect. This graph shows snow accumulation increasing during the first time period, not accumulating during the second time period, and then decreasing during the third time period; however, the question says that no snow melted (accumulation did not decrease) during this time. Choice D is incorrect. This graph shows snow accumulating at a constant rate, not stopping for a period of time or accumulating at a faster rate during a third time period.
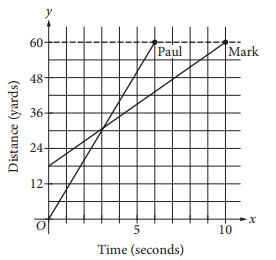
The graph above shows the positions of Paul and Mark during a race. Paul and Mark each ran at a constant rate, and Mark was given a head start to shorten the distance he needed to run. Paul finished the race in 6 seconds, and Mark finished the race in 10 seconds. According to the graph, Mark was given a head start of how many yards?
-
Solution
The lines shown on the graph give the positions of Paul and Mark during the race. At the start of the race, 0 seconds have elapsed, so the y-intercept of the line that represents Mark’s position during the race represents the number of yards Mark was from Paul’s position (at 0 yards) at the start of the race. Because the y-intercept of the line that represents Mark’s position is at the grid line that is halfway between 12 and 24, Mark had a head start of 18 yards.
Choices A, B, and D are incorrect. The y-intercept of the line that represents Mark’s position shows that he was 18 yards from Paul’s position at the start of the race, so he did not have a head start of 3, 12, or 24 yards.
Which expression is equivalent to (2x2 – 4) – (-3x2 + 2x -7)?
-
Solution
The given expression (2x2 − 4) − (−3x2 + 2x − 7) can be rewritten as 2x2 − 4 + 3x2 − 2x + 7. Combining like terms yields 5x2 − 2x + 3.
Choices B, C, and D are incorrect because they are the result of errors when applying the distributive property.
refer to the following information.
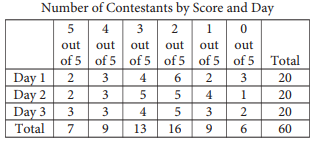
The same 20 contestants, on each of 3 days, answered 5 questions in order to win a prize. Each contestant received 1 point for each correct answer. The number of contestants receiving a given score on each day is shown in the table above.
No contestant received the same score on two different days. If a contestant is selected at random, what is the probability that the selected contestant received a score of 5 on Day 2 or Day 3, given that the contestant received a score of 5 on one of the three days?
-
Solution
The correct answer is 5⁄7. It is given that no contestant received the same score on two different days, so each of the contestants who received a score of 5 is represented in the “5 out of 5” column of the table exactly once. Therefore, the probability of selecting a contestant who received a score of 5 on Day 2 or Day 3, given that the contestant received a score of 5 on one of the three days, is found by dividing the total number of contestants who received a score of 5 on Day 2 or Day 3 (2 + 3 = 5) by the total number of contestants who received a score of 5, which is given in the table as 7. So the probability is 5⁄7. Either 5/7 or .714 can be gridded as the correct answer.
refer to the following information.

The same 20 contestants, on each of 3 days, answered 5 questions in order to win a prize. Each contestant received 1 point for each correct answer. The number of contestants receiving a given score on each day is shown in the table above.
What was the mean score of the contestants on Day 1 ?
-
Solution
The correct answer is 2.4. The mean score of the 20 contestants on
Day 1 is found by dividing the sum of the total scores of the contestants by the number of contestants. It is given that each contestant received 1 point for each correct answer. The table shows that on Day 1, 2 contestants each answered 5 questions correctly, so those 2 contestants scored 10 points in total (2 × 5 = 10). Similarly, the table shows 3 contestants each answered 4 questions correctly,
so those 3 contestants scored 12 points in total (3 × 4 = 12). Continuing these calculations reveals that the 4 contestants who answered 3 questions correctly scored 12 points in total (4 × 3 = 12); the 6 contestants who answered 2 questions correctly scored 12 points in total (6 × 2 = 12); the 2 contestants who answered
1 question correctly scored 2 points in total (2 × 1 = 2); and the 3 contestants who answered 0 questions correctly scored 0 points in total (3 × 0 = 0). Adding up the total of points scored by these 20 contestants gives 10 + 12 + 12 + 12 + 2 + 0 = 48. Therefore, the mean score of the contestants is = 2.4. Either 12/5, 2.4, or 2.40 can be gridded as the correct answer.
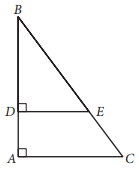
In the figure above, tan B = 3⁄4. If BC = 15 and DA = 4, what is the length of \(\overline{DE}\) ?
-
Solution
The correct answer is 6. Since tan B = 3⁄4, ΔABC and ΔDBE are both 3-4-5 triangles. This means that they are both similar to the right triangle with sides of lengths 3, 4, and 5. Since BC = 15, which is 3 times as long as the hypotenuse of the 3-4-5 triangle, the similarity ratio of ΔABC to the 3-4-5 triangle is 3:1. Therefore, the length of \(\overline{AC}\) (the side opposite to B) is 3 × 3 = 9, and the length of \(\overline{AB}\) (the side adjacent to angle B) is 4 × 3 = 12. It is also given that DA = 4. Since AB = DA + DB and AB = 12, it follows that DB = 8, which means that the similarity ratio of ΔDBE to the 3-4-5 triangle is 2:1 (\(\overline{DB}\) is the side adjacent to angle B). Therefore, the length of \(\overline{DE}\), which is the side opposite to angle B, is 3 × 2 = 6.
y = x2 – 4x + 4
y = 4 – x
If the ordered pair (x, y) satisfies the system of equations above, what is one possible value of x ?
-
Solution
The correct answer is 0 or 3. For an ordered pair to satisfy a system of equations, both the x- and y-values of the ordered pair must satisfy each equation in the system. Both expressions on the right-hand side of the given equations are equal to y, therefore it follows that both expressions on the right-hand side of the equations are equal to each other: x2 − 4x + 4 = 4 − x. This equation can be rewritten as x2 − 3x = 0, and then through factoring, the equation becomes x(x − 3) = 0. Because the product of the two factors is equal to 0, it can be concluded that either x = 0 or x – 3 = 0, or rather, x = 0 or x = 3.
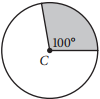
Point C is the center of the circle above. What fraction of the area of the circle is the area of the shaded region?
-
Solution
The correct answer is \(\frac{5}{18}\). There are 360° in a circle, and it is shown that the central angle of the shaded region is 100°. Therefore, the area of the shaded region can be represented as a fraction of the area of the entire circle,\(\frac{100}{360}\), which can be reduced to \(\frac{5}{18}\). Either 5/18, .277, or .288 can be gridded as the correct answer.