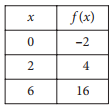
Some values of the linear function f are shown in the table above. What is the value of f(3) ?
-
Solution
A linear function has a constant rate of change, and any two rows of the shown table can be used to calculate this rate. From the first row to the second, the value of x is increased by 2 and the value of f(x) is increased by 6 = 4 − (−2). So the values of f(x) increase by 3 for every increase by 1 in the value of x. Since f(2) = 4, it follows that f(2 + 1) = 4 + 3 = 7.
Therefore, f(3) = 7. Choice A is incorrect. This is the third x-value in the table, not f(3). Choices C and D are incorrect and may result from errors when calculating the function’s rate of change.
A customer’s monthly water bill was $75.74. Due to a rate increase, her monthly bill is now $79.86. To the nearest tenth of a percent, by what percent did the amount of the customer’s water bill increase?
-
Solution
To find the percent increase of the customer’s water bill, the absolute increase of the bill, in dollars, is divided by the original amount of the bill, and the result is multiplied by 100%, as follows:
\(\frac{79.86-75.74}{75.74}\)≈0.054; 0.054 × 100% = 5.4%.
Choice A is incorrect. This choice is the difference 79.86 − 75.74 rounded to the nearest tenth, which is the (absolute) increase of the bill’s amount, not its percent increase. Choice B is incorrect and may be the result of some calculation errors. Choice C is incorrect and is the result of dividing the difference between the two bill amounts by the new bill amount instead of the original bill amount.

As part of an experiment, a ball was dropped and allowed to bounce repeatedly off the ground until it came to rest. The graph above represents the relationship between the time elapsed after the ball was dropped and the height of the ball above the ground. After it was dropped, how many times was the ball at a height of 2 feet?
-
Solution
Since the graph shows the height of the ball above the ground after it was dropped, the number of times the ball was at a height of 2 feet is equal to the number of times the graph crosses the horizontal grid line that corresponds to a height of 2 feet. The graph crosses this grid line three times.
Choices A, B, and D are incorrect. According to the graph, the ball was at a height of 2 feet three times, not one, two, or four times.
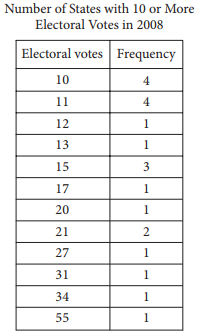
In 2008, there were 21 states with 10 or more electoral votes, as shown in the table above. Based on the table, what was the median number of electoral votes for the 21 states?
-
Solution
The median of a list of numbers is the middle value when the numbers are listed in order from least to greatest. For the electoral votes shown in the table, their frequency should also be taken into account. Since there are 21 states represented in the table, the middle number will be the eleventh number in the ordered list. Counting the frequencies from the top of the table (4 + 4 + 1 + 1 + 3 = 13) shows that the median number of electoral votes for the 21 states is 15.
Choice A is incorrect. If the electoral votes are ordered from least to greatest taking into account the frequency, 13 will be in the tenth position, not the middle. Choice C is incorrect because 17 is in the fourteenth position, not in the middle, of the ordered list. D is incorrect because 20 is in the fifteenth position, not in the middle, of the ordered list.
A study was done on the weights of different types of fish in a pond. A random sample of fish were caught and marked in order to ensure that none were weighed more than once. The sample contained 150 largemouth bass, of which 30% weighed more than 2 pounds. Which of the following conclusions is best supported by the sample data?
-
Solution
The sample of 150 largemouth bass was selected at random from all the largemouth bass in the pond, and since 30% of them weighed more than 2 pounds, it can be concluded that approximately 30% of all largemouth bass in the pond weigh more than 2 pounds.
Choices A, B, and C are incorrect. Since the sample contained 150 largemouth bass, of which 30% weighed more than 2 pounds, the largest population to which this result can be generalized is the population of the largemouth bass in the pond.
What is the sum of the solutions to (x − 6)(x + 0.7) = 0 ?
-
Solution
Since the product of x − 6 and x + 0.7 equals 0, by the zero product property either x − 6 = 0 or x + 0.7 = 0. Therefore, the solutions to the equation are 6 and −0.7. The sum of 6 and −0.7 is 5.3.
Choice A is incorrect and is the result of subtracting 6 from −0.7 instead of adding. Choice B is incorrect and may be the result of erroneously calculating the sum of −6 and 0.7 instead of 6 and −0.7. Choice D is incorrect and is the sum of 6 and 0.7, not 6 and −0.7.
refer to the following information.
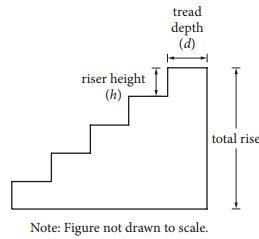
When designing a stairway, an architect can use the riser-tread formula 2 + = 25 h d , where h is the riser height, in inches, and d is the tread depth, in inches. For any given stairway, the riser heights are the same and the tread depths are the same for all steps in that stairway. The number of steps in a stairway is the number of its risers. For example, there are 5 steps in the stairway in the figure above. The total rise of a stairway is the sum of the riser heights as shown in the figure.
An architect wants to use the riser-tread formula to design a stairway with a total rise of 9 feet, a riser height between 7 and 8 inches, and an odd number of steps. With the architect’s constraints, which of the following must be the tread depth, in inches, of the stairway? (1 foot = 12 inches)
-
Solution
Let h be the riser height, in inches, and n be the number of the steps in the stairway. According to the architect’s design, the total rise of the stairway is 9 feet, or 9 × 12 = 108 inches. Hence, nh = 108, and solving for n gives n = \(\frac{108}{h}\). It is given that 7 < h < 8. It follows that \(\frac{108}{8} < \frac{108}{h} < \frac{108}{7}\). Since \(\frac{108}{8} < 14\) and \(\frac{108}{7} < 15\) and n is an integer, it follows that 14 ≤ n ≤ 15. Since n can be an odd number, n can only be 15; therefore, \(h = \frac{108}{15} = 7.2\) inches. Substituting 7.2 for h in the riser-tread formula 2h + d = 25 gives 14.4 + d = 25. Solving for d gives d = 10.6 inches.
Choice A is incorrect because 7.2 inches is the riser height, not the tread depth of the stairs. Choice B is incorrect and may be the result of calculation errors. Choice D is incorrect because 15 is the number of steps, not the tread depth of the stairs.
refer to the following information.

When designing a stairway, an architect can use the riser-tread formula 2 + = 25 h d , where h is the riser height, in inches, and d is the tread depth, in inches. For any given stairway, the riser heights are the same and the tread depths are the same for all steps in that stairway. The number of steps in a stairway is the number of its risers. For example, there are 5 steps in the stairway in the figure above. The total rise of a stairway is the sum of the riser heights as shown in the figure.
Some building codes require that, for indoor stairways, the tread depth must be at least 9 inches and the riser height must be at least 5 inches. According to the riser-tread formula, which of the following inequalities represents the set of all possible values for the riser height that meets this code requirement?
-
Solution
Since the tread depth, d, must be at least 9 inches, and the riser height, h, must be at least 5 inches, it follows that d ≥ 9 and h ≥ 5, respectively. Solving for d in the risertread formula 2h + d = 25 gives d = 25 − 2h. Thus the first inequality, d ≥ 9, is equivalent to 25 − 2h ≥ 9. This inequality can be solved for h as follows:
−2h ≥ 9 − 25
2h ≤ 25 − 9
2h ≤ 16
h ≤ 8
Therefore, the inequality 5 ≤ h ≤ 8, derived from combining the inequalities h ≥ 5 and h ≤ 8,represents the set of all possible values for the riser height that meets the code requirement.
Choice A is incorrect because the riser height, h, cannot be less than 5 inches. Choices B and D are incorrect because the riser height, h, cannot be greater than 8. For example, if h = 10, then according to the riser-tread formula 2h + d = 25, it follows that d = 5 inches. However, d must be at least 9 inches according to the building codes, so h cannot be 10.
refer to the following information.

When designing a stairway, an architect can use the riser-tread formula 2 + = 25 h d , where h is the riser height, in inches, and d is the tread depth, in inches. For any given stairway, the riser heights are the same and the tread depths are the same for all steps in that stairway. The number of steps in a stairway is the number of its risers. For example, there are 5 steps in the stairway in the figure above. The total rise of a stairway is the sum of the riser heights as shown in the figure.
Which of the following expresses the riser height in terms of the tread depth?
-
Solution
Isolating the term that contains the riser height, h, in the formula 2h + d = 25 gives 2h = 25 − d. Dividing both sides of this equation by 2 yields h = \(\frac{25-d}{2}\), or h = 1⁄2(25 - d).
Choices A, C, and D are incorrect and may result from incorrect transformations of the risertread formula 2h + d = 25 when expressing h in terms of d.
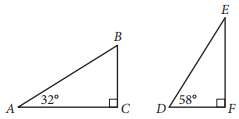
Triangles ABC and DEF are shown above. Which of the following is equal to the ratio \(\frac{BC}{AB}\)?
-
Solution
In right triangle ABC, the measure of angle B must be 58° because the sum of the measure of angle A, which is 32°, and the measure of angle B is 90°. Angle D in the right triangle DEF has measure 58°. Hence, triangles ABC and DEF are similar. Since BC is the side opposite to the angle with measure 32° and AB is the hypotenuse in right triangle ABC, the ratio opposite to the angle with measure 32° and AB is the hypotenuse in right triangle ABC, the ratio \(\frac{BC}{AB}\) is equal to \(\frac{DF}{DE}\).
Alternate approach: The trigonometric ratios can be used to answer this question. In right triangle ABC, the ratio \(\frac{BC}{AB}\) = sin(32°). The angle E in triangle DEF has measure 32° because m(∠D) + m(∠D) = 90°. In triangle DEF, the ratio sin(32°) \(\frac{DF}{DE}\). Therefore,\(\frac{DF}{DE}=\frac{BC}{AB}\).
Choice A is incorrect because \(\frac{DE}{DF}\) is the inverse of the ratio \(\frac{BC}{AB}\). Choice C is incorrect because \(\frac{DF}{EF}=\frac{BC}{AC}\), not \(\frac{BC}{AB}\). Choice D is incorrect because \(\frac{EF}{DE}=\frac{AC}{AB}\), not \(\frac{BC}{AB}\).