refer to the following information.
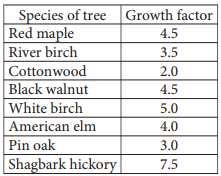
One method of calculating the approximate age, in years, of a tree of a particular species is to multiply the diameter of the tree, in inches, by a constant called the growth factor for that species. The table above gives the growth factors for eight species of trees.
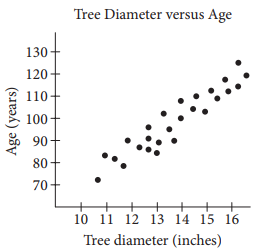
The scatterplot above gives the tree diameter plotted against age for 26 trees of a single species. The growth factor of this species is closest to that of which of the following species of tree?
-
Solution
The growth factor of a tree species is approximated by the slope of a line of best fit that models the relationship between diameter and age. A line of best fit can be visually estimated by identifying a line that goes in the same direction of the data and where roughly half the given data points fall above and half the given data points fall below the line. Two points that fall on the line can be used to estimate the slope and y-intercept of the equation of a line of best fit. Estimating a line of best fit for the given scatterplot could give the points (11, 80) and (15, 110). Using these two points, the slope of the equation of the line of best fit can be calculated as \(\frac{110-80}{15-11}\), or 7.5. The slope of the equation is interpreted as the growth factor for a species of tree. According to the table, the species of tree with a growth factor of 7.5 is shagbark hickory.
Choices A, B, and C are incorrect and likely result from errors made when estimating a line of best fit for the given scatterplot and its slope.
refer to the following information.

One method of calculating the approximate age, in years, of a tree of a particular species is to multiply the diameter of the tree, in inches, by a constant called the growth factor for that species. The table above gives the growth factors for eight species of trees.
According to the information in the table, what is the approximate age of an American elm tree with a diameter of 12 inches?
-
Solution
According to the given information, multiplying a tree species’ growth factor by the tree’s diameter is a method to approximate the age of the tree. Multiplying the growth factor, 4.0, of the American elm given in the table by the given diameter of 12 inches yields an approximate age of 48 years.
Choices A, B, and C are incorrect because they do not result from multiplying the given diameter of an American elm tree with that tree species’ growth factor..
A polling agency recently surveyed 1,000 adults who were selected at random from a large city and asked each of the adults, “Are you satisfied with the quality of air in the city?” Of those surveyed, 78 percent responded that they were satisfied with the quality of air in the city. Based on the results of the survey, which of the following statements must be true?
I. Of all adults in the city, 78 percent are satisfied with the quality of air in the city.
II. If another 1,000 adults selected at random from the city were surveyed, 78 percent of them would report they are satisfied with the quality of air in the city.
III. If 1,000 adults selected at random from a different city were surveyed, 78 percent of them would report they are satisfied with the quality of air in the city.
-
Solution
Statement I need not be true. The fact that 78% of the 1,000 adults who were surveyed responded that they were satisfied with the air quality in the city does not mean that the exact same percentage of all adults in the city will be satisfied with the air quality in the city. Statement II need not be true because random samples, even when they are of the same size, are not necessarily identical with regard to percentages of people in them who have a certain opinion. Statement III need not be true for the same reason that statement II need not be true: results from different samples can vary. The variation may be even bigger for this sample since it would be selected from a different city. Therefore, none of the statements must be true.
Choices B, C, and D are incorrect because none of the statements must be true.

In a survey, 607 general surgeons and orthopedic surgeons indicated their major professional activity. The results are summarized in the table above. If one of the surgeons is selected at random, which of the following is closest to the probability that the selected surgeon is an orthopedic surgeon whose indicated professional activity is research?
-
Solution
According to the table, 74 orthopedic surgeons indicated that research is their major professional activity. Since a total of 607 surgeons completed the survey, it follows that the probability that the randomly selected surgeon is an orthopedic surgeon whose indicated major professional activity is research is 74 out of 607, or 74/607, which is ≈ 0.122.
Choices B, C, and D are incorrect and may be the result of finding the probability that the randomly selected surgeon is an orthopedic surgeon whose major professional activity is teaching (choice B), an orthopedic surgeon whose major professional activity is either teaching or research (choice C), or a general surgeon or orthopedic surgeon whose major professional activity is research (choice D).
y ≤ 3x + 1
x – y > 1
Which of the following ordered pairs (x, y) satisfies the system of inequalities above?
-
Solution
Any point (x, y) that is a solution to the given system of inequalities must satisfy both inequalities in the system. Since the second inequality in the system can be rewritten as y < x − 1, the system is equivalent to the following system.
y ≤ 3x + 1
y < x - 1
Since 3x + 1 > x − 1 for x > −1 and 3x + 1 ≤ x − 1 for x ≤ −1, it follows that y < x − 1 for x > −1 and y ≤ 3x + 1 for x ≤ −1. Of the given choices, only (2, −1) satisfies these conditions because −1 < 2 − 1 = 1.
Alternate approach: Substituting (2, −1) into the first inequality gives −1 ≤ 3(2) + 1, or −1 ≤ 7, which is a true statement. Substituting (2, −1) into the second inequality gives 2 − (−1) > 1, or 3 > 1, which is a true statement. Therefore, since (2, −1) satisfies both inequalities, it is a solution to the system.
Choice A is incorrect because substituting −2 for x and −1 for y in the first inequality gives −1 ≤ 3(−2) + 1, or −1 ≤ −5, which is false. Choice B is incorrect because substituting −1 for x and 3 for y in the first inequality gives 3 ≤ 3(−1) + 1, or 3 ≤ −2, which is false. Choice C is incorrect because substituting 1 for x and 5 for y in the first inequality gives 5 ≤ 3(1) + 1, or 5 ≤ 4, which is false.
1⁄2y = 4
x – 1⁄2y = 2
The system of equations above has solution (x, y).What is the value of x ?
-
Solution
Adding the two equations side by side eliminates y and yields x = 6, as shown.

If (x, y) is a solution to the system, then (x, y) satisfies both equations in the system and any equation derived from them. Therefore, x = 6.
Choices A, B, and C are incorrect and may be the result of errors when solving the system.
−2 + 3 = 6 x y
In the xy-plane, the graph of which of the following equations is perpendicular to the graph of the equation above?
-
Solution
The equation −2x + 3y = 6 can be rewritten in the slope-intercept form as follows: y = 2⁄3 x + 2. So the slope of the graph of the given equation is 2⁄3. In the xy-plane, when two nonvertical lines are perpendicular, the product of their slopes is −1. So, if m is the slope of a line perpendicular to the line with equation y =2⁄3 x + 2, then m × 2⁄3 = −1, which yields m = - 3⁄2. Of the given choices, only the equation in choice A can be rewritten in the form y = 3⁄2 x + b, for some constant b. Therefore, the graph of the equation in choice A is perpendicular to the graph of the given equation.
Choices B, C, and D are incorrect because the graphs of the equations in these choices have slopes, respectively, of - 3⁄4,- 1⁄2, and -1⁄3, not 3⁄2.
The density d of an object is found by dividing the mass m of the object by its volume V. Which of the following equations gives the mass m in terms of d and V ?
-
Solution
The density d of an object can be found by dividing the mass m of the object by its volume V. Symbolically this is expressed by the equation d = m⁄v. Solving this equation for m yields m = dV.
Choices B, C, and D are incorrect and are likely the result of errors made when translating the definition of density into an algebraic equation and errors made when solving this equation for m. If the equations given in choices B, C, and D are each solved for density d, none of the resulting equations are equivalent to d = m⁄v.
In the 1908 Olympic Games, the Olympic marathon was lengthened from 40 kilometers to approximately 42 kilometers. Of the following, which is closest to the increase in the distance of the Olympic marathon, in miles? (1 mile is approximately 1.6 kilometers.)
-
Solution
In 1908, the marathon was lengthened by 42 − 40 = 2 kilometers. Since 1 mile is approximately 1.6 kilometers, the increase of 2 kilometers can be converted to miles by multiplying as shown: 2kilometers×\(\frac{1\, mile}{1.6\, kilometers}=1.25miles\)
Choices A, C, and D are incorrect and may result from errors made when applying the conversion rate or other computational errors.
Which of the following is an equivalent form of (1.5x − 2.4)2 − (5.2x2 − 6.4)?
-
Solution
The first expression (1.5x − 2.4)2 can be rewritten as (1.5x − 2.4)(1.5x − 2.4).Applying the distributive property to this product yields (2.25x2 − 3.6x − 3.6x + 5.76) − (5.2x2−6.4). This difference can be rewritten as (2.25x2− 3.6x − 3.6x + 5.76) + (−1)(5.2x2− 6.4). Distributing the factor of −1 through the second expression yields 2.25x2− 3.6x − 3.6x + 5.76 − 5.2x2 + 6.4. Regrouping like terms, the expression becomes (2.25x2− 5.2x2) + (−3.6x − 3.6x) + (5.76 + 6.4). Combining like terms yields −2.95x2 − 7.2x + 12.16.
Choices A, B, and D are incorrect and likely result from errors made when applying the distributive property or combining the resulting like terms.
