refer to the following information.
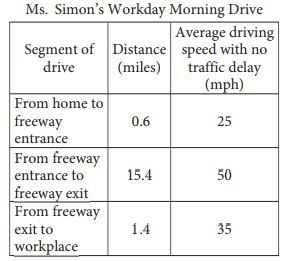
Ms. Simon drives her car from her home to her workplace every workday morning. The table above shows the distance, in miles, and her average driving speed, in miles per hour (mph), when there is no traffic delay, for each segment of her drive.
One morning, Ms. Simon drove directly from her home to her workplace in 24 minutes. What was her average speed, in miles per hour, during her drive that morning?
-
Solution
The correct answer is 43.5, 43, or 44. The distance from Ms. Simon’s home to her workplace is 0.6 + 15.4 + 1.4 = 17.4 miles. Ms. Simon took 24 minutes to drive this distance. Since there are 60 minutes in one hour, her average speed, in miles per hour, for this trip is \(\frac{17.4}{24}\) × 60= 43.5 miles per hour. Based on the directions, 87/2 or 43.5 can be gridded as the correct answer. We are accepting 43 and 44 as additional correct answers because the precision of the measurements provided does not support an answer with three significant digits.
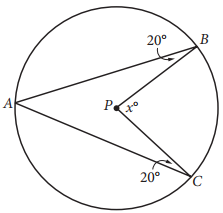
Point P is the center of the circle in the figure above. What is the value of x ?
-
Solution
The correct answer is 80. The measure of an angle inscribed in a circle is half the measure of the central angle that intercepts the same arc. That is, mÐA = x°⁄2. Also, the sum of the interior angles of quadrilateral ABCP is 360°, and the measure of the obtuse angle P is 360° − x°. Hence,x°⁄2 + 20° + (360° − x°) + 20° = 360°. Simplifying this equation gives x°⁄2 = 40, and so x = 80.
Alternate approach: If points A and P are joined, then the triangles that will be formed, APB and APC, are isosceles because PA = PB = PC. It follows that the base angles on both triangles each have measure of 20°. Angle A consists of two base angles, and therefore, m∠A = 40°. Since the measure of an angle inscribed in a circle is half the measure of the central angle that intercepts the same arc, it follows that the value of x is 80°.
A landscaper is designing a rectangular garden. The length of the garden is to be 5 feet longer than the width. If the area of the garden will be 104 square feet, what will be the length, in feet, of the garden?
-
Solution
The correct answer is 13. Let w represent the width of the rectangular garden, in feet. Since the length of the garden will be 5 feet longer than the width of the garden, the length of the garden will be w + 5 feet. Thus the area of the garden will be w(w + 5). It is also given that the area of the garden will be 104 square feet. Therefore, w(w + 5) = 104, which is equivalent to w2 + 5w − 104 = 0. The quadratic formula can be used or the equation above can be factored to result in (w + 13)(w − 8) = 0. Therefore, w = 8 and w = −13. Because width cannot be negative, the width of the garden must be 8 feet. This means the length of the garden must be 8 + 5 = 13 feet.
In the xy-plane, the point (2, 5) lies on the graph of the function f. If f(x) = k – x2, where k is a constant, what is the value of k ?
-
Solution
The correct answer is 9. Since the point (2, 5) lies on the graph of y = f(x) in the xy-plane, the ordered pair (2, 5) must satisfy the equation y = f(x). That is, 5 = f(2), or 5 = k − 22. This equation simplifies to 5 = k − 4. Therefore, the value of the constant k is 9
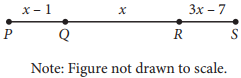
On \(\overline{PS}\) above, PQ = RS. What is the length of \(\overline{PS}\) ?
-
Solution
The correct answer is 7. It is given that PQ = RS, and the diagram shows that PQ = x − 1 and RS = 3x − 7. Therefore, the equation x − 1 = 3x − 7 must be true. Solving this equation for x leads to 2x = 6, so x = 3. The length of segment PS is the sum of the lengths of PQ, QR, and RS, which is (x − 1) + x + (3x − 7), or equivalently 5x − 8. Substituting 3 for x in this expression gives 5(3) − 8 = 7.
The painting The Starry Night by Vincent van Gogh is rectangular in shape with height 29 inches and width 36.25 inches. If a reproduction was made where each dimension is 1⁄3 the corresponding original dimension, what is the height of the reproduction, in inches?
-
Solution
The correct answer is \(\frac{29}{3}\). It is given that the height of the original painting is 29 inches and the reproduction’s height is 1⁄3 the original height. One-third of 29 is \(\frac{29}{3}\), or 9.\(\bar{6}\). Either the fraction 29/3 or the decimals 9.66 or 9.67 can be gridded as the correct answer.
Horsepower and watts are units of measure of power. They are directly proportional such that 5 horsepower is equal to 3730 watts. How much power, in watts, is equal to 2 horsepower?
-
Solution
The correct answer is 1492. Let x be the number of watts that is equal to 2 horsepower. Since 5 horsepower is equal to 3730 watts, it follows that 2⁄5=\(\frac{x}{3730}\). Solving this proportion for x yields 5x = 7460, or x =\(\frac{7460}{5}\)= 1492.
y = x2 − a
In the equation above, a is a positive constant and the graph of the equation in the xy‑plane is a parabola. Which of the following is an equivalent form of the equation?
-
Solution
The given equation can be thought of as the difference of two squares, where one square is x2 and the other square is (√a)2. Using the difference of squares formula,the equation can be rewritten as y = (x + √a)(x - √a).
Choices A, C, and D are incorrect because they are not equivalent to the given equation. Choice A is incorrect because it is equivalent to y = x2 − a2. Choice C is incorrect because it is equivalent to y = x2 - a2⁄4. Choice D is incorrect because it is equivalent to y = x2 + 2ax + a2.
x2 + 20x + y2 + 16y = −20
The equation above defines a circle in the xy-plane. What are the coordinates of the center of the circle?
-
Solution
The standard equation of a circle in the xy-plane is of the form (x − h)2 + (y − k)2 = r2, where (h, k) are the coordinates of the center of the circle and r is the radius. To convert the given equation to the standard form, complete the squares. The first two terms need a 100 to complete the square, and the second two terms need a 64. Adding 100 and 64 to both sides of the given equation yields (x2 + 20x + 100) + (y2 + 16y + 64) = −20 + 100 + 64, which is equivalent to (x + 10)2 + (y + 8)2 = 144. Therefore, the coordinates of the center of the circle are (−10, −8).
Choice A is incorrect and is likely the result of not properly dividing when attempting to complete the square. Choice C is incorrect and is likely the result of making a sign error when evaluating the coordinates of the center. Choice D is incorrect and is likely the result of not properly dividing when attempting to complete the square and making a sign error when evaluating the coordinates of the center.
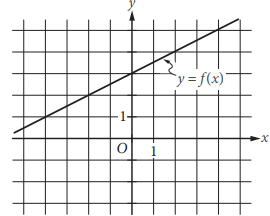
The graph of the linear function f is shown in the xy-plane above. The slope of the graph of the linear function g is 4 times the slope of the graph of f. If the graph of g passes through the point (0, −4), what is the value of g(9) ?
-
Solution

