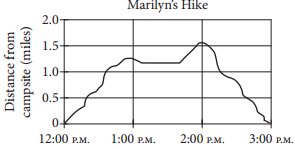
The graph above shows Marilyn’s distance from her campsite during a 3‑hour hike. She stopped for 30 minutes during her hike to have lunch. Based on the graph, which of the following is closest to the time she finished lunch and continued her hike?
-
Solution
Marilyn’s distance from her campsite remained the same during the time she ate lunch. This is represented by a horizontal segment in the graph. The only horizontal segment in the graph starts at a time of about 1:10 p.m. and ends at about 1:40 p.m. Therefore, Marilyn finished her lunch and continued her hike at about 1:40 p.m.
Choices A, B, and D are incorrect and may be the result of a misinterpretation of the graph. For example, choice B is the time Marilyn started her lunch, and choice D is the time Marilyn was at the maximum distance from her campsite.
refer to the following information.
The stock price of one share in a certain company is worth $360 today. A stock analyst believes that the stock will lose 28 percent of its value each week for the next three weeks. The analyst uses the equation V = 360(r)t to model the value, V, of the stock after t weeks.
To the nearest dollar, what does the analyst believe the value of the stock will be at the end of three weeks? (Note: Disregard the $ sign when gridding your answer.)
-
Solution
The correct answer is 134. The analyst’s prediction is that the stock will lose 28 percent of its value for each of the next three weeks. Thus, the predicted value of the stock after 1 week is $360 − (0.28)$360 = $259.20; after 2 weeks, $259.20 − (0.28)$259.20 ≈ $186.62; and after 3 weeks, $186.62 − (0.28)$186.62 ≈ $134.37. Therefore, to the nearest dollar, the stock analyst believes the stock will be worth 134 dollars after three weeks.
refer to the following information.
The stock price of one share in a certain company is worth $360 today. A stock analyst believes that the stock will lose 28 percent of its value each week for the next three weeks. The analyst uses the equation V = 360(r)t to model the value, V, of the stock after t weeks.
What value should the analyst use for r ?
-
Solution
The correct answer is .72. According to the analyst’s estimate, the value V, in dollars, of the stock will decrease by 28% each week for t weeks, where t = 1, 2, or 3, with its value being given by the formula V = 360(r)t . This equation is an example of exponential decay. A stock losing 28% of its value each week is the same as the stock’s value decreasing to 72% of its value from the previous week, since V − (.28)V = (.72)V. Using this information, after 1 week the value, in dollars, of the stock will be V = 360(.72); after 2 weeks the value of the stock will be V = 360(.72)(.72) = 360(.72)2 ; and after 3 weeks the value of the stock will be V = 360(.72)(.72)(.72) = 360(.72)3. For all of the values of t in question, namely t = 1, 2, and 3, the equation V = 360(.72)t is true. Therefore, the analyst should use .72 as the value of r.
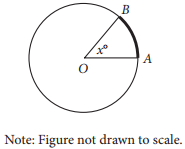
In the figure above, the circle has center O and has radius 10. If the length of arc \(\overset{\frown}{AB}\) (shown in bold) is between 5 and 6, what is one possible integer value of x ?
-
Solution
The correct answer is 29, 30, 31, 32, 33, or 34. Since the radius of the circle is 10, its circumference is 20π. The full circumference of a circle is 360°.Thus, an arc of length s on the circle corresponds to a central angle of x°,where \(\frac{x}{360}=\frac{s}{20\pi }\), or x = \(\frac{360}{20\pi }\) s. Since 5 < s < 6, it follows that \(\frac{360}{20\pi }\) (5) < x < \(\frac{360}{20\pi }\)(6), which becomes, to the nearest tenth, 28.6 < x < 34.4. Therefore, the possible integer values of x are 29, 30, 31, 32, 33, and 34. Any one of these numbers may be gridded as the correct answer.
q = 1⁄2nv2
The dynamic pressure q generated by a fluid moving with velocity v can be found using the formula above, where n is the constant density of the fluid. An aeronautical engineer uses the formula to find the dynamic pressure of a fluid moving with velocity v and the same fluid moving with velocity 1.5v. What is the ratio of the dynamic pressure of the faster fluid to the dynamic pressure of the slower fluid?
-
Solution
The correct answer is 2.25 or 9⁄4. Let qs be the dynamic pressure of the slower fluid moving with velocity vs , and let qf be the dynamic pressure of the faster fluid moving with velocity vf. Then vf = 1.5vs.
Given the equation q = 1⁄2 nv2, substituting the dynamic pressure and velocity of the faster fluid gives qf = 1⁄2nv\(_{f}^{2}\). Since vf = 1.5vs, the expression 1.5vs can be substituted for vf in this equation, giving qf = 1⁄2n(1.5vs)2.This can be rewritten as qf = (2.25)1⁄2nv\(_{s}^{2}\) =(2.25)qs. Therefore, the ratio of the dynamic pressure of the faster fluid is \(\frac{q_{f}}{q_{s}}=\frac{2.25q_{s}}{q_{s}}\) = 2.25. Either 2.25 or the equivalent improper fraction 9⁄4 may be gridded as the correct answer.
In a study of bat migration habits, 240 male bats and 160 female bats have been tagged. If 100 more female bats are tagged, how many more male bats must be tagged so that 3⁄5 of the total number of bats in the study are male?
-
Solution
The correct answer is 150. In the study, 240 male and 160 plus another 100 female bats have been tagged, so that 500 bats have been tagged altogether.If x more male bats must be tagged for 3⁄5 of the total number of bats to be male, the proportion \(\frac{male\, bats}{total\, bats}\) = \(\frac{240 + x}{500 + x}\) = 3⁄5 must be true. Multiplying each side of\(\frac{240 + x}{500 + x}=\frac{3}{5}\) by 5(500 + x) gives 5(240 + x) = 3(500 + x), which simplifies to 1200 + 5x = 1500 + 3x. Therefore, x = 150, and 150 more male bats must be tagged; this will bring the total to 390 male bats out of 650 bats, which is equal to 3⁄5
The pes, a Roman measure of length, is approximately equal to 11.65 inches. It is also equivalent to 16 smaller Roman units called digits. Based on these relationships, 75 Roman digits is equivalent to how many feet, to the nearest hundredth? (12 inches = 1 foot)
-
Solution
The correct answer is 4.55. Since there are 16 Roman digits in a Roman pes, 75 digits is equal to \(\frac{75}{16}\) pes. Since 1 pes is equal to 11.65 inches, \(\frac{75}{16}\) pes is equal to \(\frac{75}{16}\)(11.65) inches. Since 12 inches is equal to 1 foot,\(\frac{75}{16}\)(11.65) inches is equal to \(\frac{75}{16}\)(11.65)(\(\frac{1}{12}\)) 4.55078125 feet. Therefore, 75 digits is equal to \(\frac{75}{16}\)(11.65)(\(\frac{1}{12}\) = 4.55078125 feet. Rounded to the nearest hundredth of a foot, 75 Roman digits is equal to 4.55 feet.
The normal systolic blood pressure P, in millimeters of mercury, for an adult male x years old can be modeled by the equation P = \(\frac{x + 220}{2}\). According to the model, for every increase of 1 year in age, by how many millimeters of mercury will the normal systolic blood pressure for an adult male increase?
-
Solution
The correct answer is 1⁄2 or .5. The equation that models the normal systolic blood pressure, in millimeters of mercury, for a male x years old,P = \(\frac{x + 220}{2}\), can be rewritten as P = 1⁄2x + 110. For each increase of 1 year in age, the value of x increases by 1; hence, P becomes 1⁄2 (x + 1) + 110 = (1⁄2x + 110) + 1⁄2. That is, P increases by 1⁄2 millimeter of mercury. Either the fraction 1⁄2 or its decimal equivalent, .5, may be gridded as the correct answer
A partially filled pool contains 600 gallons of water. A hose is turned on, and water flows into the pool at the rate of 8 gallons per minute. How many gallons of water will be in the pool after 70 minutes?
-
Solution
The correct answer is 1160. The pool contains 600 gallons of water before the hose is turned on, and water flows from the hose into the pool at a rate of 8 gallons per minute. Thus, the number of gallons of water in the pool m minutes after the hose is turned on is given by the expression 600 + 8m. Therefore, after 70 minutes, there will be 600 + 8(70) = 1160 gallons of water in the pool.
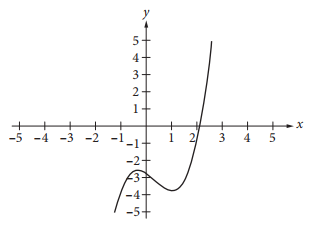
The function f(x) = x3 − x2 – x – \(\frac{11}{4}\) is graphed in the xy-plane above. If k is a constant such that the equation f(x) = k has three real solutions, which of the following could be the value of k ?
-
Solution
The equation f(x) = k gives the solutions to the system of equations y = f(x) = x3 − x2 − x − \(\frac{11}{4}\) and y = k. A real solution of a system of two equations corresponds to a point of intersection of the graphs of the two equations in the xy-plane. The graph of y = k is a horizontal line that contains the point (0, k). Thus, the line with equation y = −3 is a horizontal line that intersects the graph of the cubic equation three times, and it follows that the equation f(x) = −3 has three real solutions.
Choices A, B, and C are incorrect because the graphs of the corresponding equations are horizontal lines that do not intersect the graph of the cubic equation three times.