refer to the following information.

The chart above shows approximations of the acceleration due to gravity in meters per second squared \(\left ( \frac{m}{sec^{2}} \right )\) for the eight planets in our solar system. The weight of an object on a given planet can be found by using the formula W mg = , where W is the weight of the object measured in newtons, m is the mass of the object measured in kilograms, and g is the acceleration due to gravity on the planet measured in \(\frac{m}{sec^{2}}\).
An object on Earth has a weight of 150 newtons. On which planet would the same object have an approximate weight of 170 newtons?
-
Solution
On Earth, the acceleration due to gravity is 9.8 m/sec2. Thus, for an object with a weight of 150 newtons, the formula W = mg becomes 150 = m(9.8), which shows that the mass of an object with a weight of 150 newtons on Earth is about 15.3 kilograms. Substituting this mass into the formula W = mg and now using the weight of 170 newtons gives 170 = 15.3g, which shows that the second planet’s acceleration due to gravity is about 11.1 m/sec2. According to the table, this value for the acceleration due to gravity holds on Saturn.
Choices A, C, and D are incorrect. Using the formula W = mg and the values for g in the table shows that an object with a weight of 170 newtons on these planets would not have the same mass as an object with a weight of 150 newtons on Earth.
refer to the following information.

The chart above shows approximations of the acceleration due to gravity in meters per second squared \(\left ( \frac{m}{sec^{2}} \right )\) for the eight planets in our solar system. The weight of an object on a given planet can be found by using the formula W mg = , where W is the weight of the object measured in newtons, m is the mass of the object measured in kilograms, and g is the acceleration due to gravity on the planet measured in \(\frac{m}{sec^{2}}\).
What is the weight, in newtons, of an object on Mercury with a mass of 90 kilograms?
-
Solution
On Mercury, the acceleration due to gravity is 3.6 m/sec2. Substituting 3.6 for g and 90 for m in the formula W = mg gives W = 90(3.6) = 324 newtons.
Choice A is incorrect and may be the result of dividing 90 by 3.6. Choice B is incorrect and may be the result of subtracting 3.6 from 90 and rounding to the nearest whole number. Choice C is incorrect because an object with a weight of 101 newtons on Mercury would have a mass of about 28 kilograms, not 90 kilograms.
Nate walks 25 meters in 13.7 seconds. If he walks at this same rate, which of the following is closest to the distance he will walk in 4 minutes?
-
Solution
Because Nate walks 25 meters in 13.7 seconds, and 4 minutes is equal to 240 seconds, the proportion \(\frac{25\, meters}{13.7\, sec}=\frac{x\, meters}{240\, sec}\) can be used to find out how many meters, x, Nate walks in 4 minutes. The proportion can be simplified to \(\frac{25}{13.7}=\frac{x}{240}\), because the units of meters per second cancel, and then each side of the equation can be multiplied by 240, giving \(\frac{(240)(25)}{13.7}\) = x ≈ 438. Therefore, of the given options, 450 meters is closest to the distance Nate will walk in 4 minutes.
Choice A is incorrect and may be the result of setting up the proportion as \(\frac{13.7\, sec}{25\, meters}=\frac{x\, meters}{240\, sec}\) and finding that x ≈ 132, which is close to 150.Choices C and D are incorrect and may be the result of errors in calculation.
The average number of students per classroom at Central High School from 2000 to 2010 can be modeled by the equation y = 0.56 + 27.2 x , where x represents the number of years since 2000, and y represents the average number of students per classroom. Which of the following best describes the meaning of the number 0.56 in the equation?
-
Solution
In the equation y = 0.56x + 27.2, the value of x increases by 1 for each year that passes. Each time x increases by 1, y increases by 0.56 since 0.56 is the slope of the graph of this equation. Since y represents the average number of students per classroom in the year represented by x, it follows that, according to the model, the estimated increase each year in the average number of students per classroom at Central High School is 0.56.
Choice A is incorrect because the total number of students in the school in 2000 is the product of the average number of students per classroom and the total number of classrooms, which would appropriately be approximated by the y-intercept (27.2) times the total number of classrooms, which is not given. Choice B is incorrect because the average number of students per classroom in 2000 is given by the y-intercept of the graph of the equation, but the question is asking for the meaning of the number 0.56, which is the slope. Choice D is incorrect because 0.56 represents the estimated yearly change in the average number of students per classroom. The estimated difference between the average number of students per classroom in 2010 and 2000 is 0.56 times the number of years that have passed between 2000 and 2010, that is, 0.56 × 10 = 5.6.
If 3⁄5 w = 4⁄2, what is the value of w ?
-
Solution
To solve the equation for w, multiply both sides of the equation by the reciprocal of 3⁄5, which is 5⁄3. This gives (5⁄3)·3⁄5w =4⁄5· (5⁄3),which simplifies to w = \(\frac{20}{9}\).
Choices A, B, and C are incorrect and may be the result of errors in arithmetic when simplifying the given equation.
3x2 − 5x + 2
5x2 − 2x − 6
Which of the following is the sum of the two polynomials shown above?
-
Solution
The sum of the two polynomials is (3x2 − 5x + 2) + (5x2 − 2x − 6). This can be rewritten by combining like terms: (3x2 − 5x + 2) + (5x2 − 2x − 6) = (3x2 + 5x2) + (−5x − 2x) + (2 − 6) = 8x2 − 7x − 4.
Choice B is incorrect and may be the result of a sign error when combining the coefficients of the x-term. Choice C is incorrect and may be the result of adding the exponents, as well as the coefficients, of like terms. Choice D is incorrect and may be the result of a combination of the errors described in B and C.
At Lincoln High School, approximately 7 percent of enrolled juniors and 5 percent of enrolled seniors were inducted into the National Honor Society last year. If there were 562 juniors and 602 seniors enrolled at Lincoln High School last year, which of the following is closest to the total number of juniors and seniors at Lincoln High School last year who were inducted into the National Honor Society?
-
Solution
Since 7 percent of the 562 juniors is 0.07(562) and 5 percent of the 602 seniors is 0.05(602), the expression 0.07(562) + 0.05(602) can be evaluated to determine the total number of juniors and seniors inducted into the honor society. Of the given choices, 69 is closest to the value of the expression.
Choice A is incorrect and may be the result of adding the number of juniors and seniors and the percentages given and then using the expression (0.07 + 0.05)(562 + 602). Choices C and D are incorrect and may be the result of finding either only the number of juniors inducted or only the number of seniors inducted.
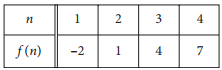
The table above shows some values of the linear function f. Which of the following defines f ?
-
Solution
The graph of y = f(n) in the coordinate plane is a line that passes through each of the points given in the table. From the table, one can see that an increase of 1 unit in n results in an increase of 3 units in f(n); for example, f(2) − f(1) = 1 − (−2) = 3. Therefore, the graph of y = f(n) in the coordinate plane is a line with slope 3. Only choice C is a line with slope 3. The y-intercept of the line is the value of f(0). Since an increase of 1 unit in n results in an increase of 3 units in f(n), it follows that f(1) − f(0) = 3. Since f(1) = −2, it follows that f(0) = f(1) − 3 = −5. Therefore, the y-intercept of the graph of f(n) is −5, and the slope-intercept equation for f(n) is f(n) = 3n − 5.
Choices A, B, and D are incorrect because each equation has the incorrect slope of the line (the y-intercept in each equation is also incorrect).
The graph below shows the total number of music album sales, in millions, each year from 1997 through 2009.
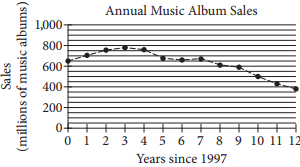
Based on the graph, which of the following best describes the general trend in music album sales from 1997 through 2009 ?
-
Solution
Based on the graph, sales increased in the first 3 years since 1997, which is until year 2000, and then generally decreased thereafter.
Choices A, B, and D are incorrect; each of these choices contains inaccuracies in describing the general trend of music album sales from 1997 to 2000.
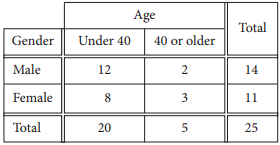
The table above shows the distribution of age and gender for 25 people who entered a contest. If the contest winner will be selected at random, what is the probability that the winner will be either a female under age 40 or a male age 40 or older?
-
Solution
Of the 25 people who entered the contest, there are 8 females under age 40 and 2 males age 40 or older. Therefore, the probability that the contest winner will be either a female under age 40 or a male age 40 or older is \(\frac{8}{25}+\frac{2}{25}=\frac{10}{25}\).
Choice A is incorrect and may be the result of dividing 8 by 2, instead of adding 8 to 2, to find the probability. Choice C is incorrect; it is the probability that the contest winner will be either a female under age 40 or a female age 40 or older. Choice D is incorrect and may be the result of multiplying 8 and 2, instead of adding 8 and 2, to find the probability.