A researcher conducted a survey to determine whether people in a certain large town prefer watching sports on television to attending the sporting event. The researcher asked 117 people who visited a local restaurant on a Saturday, and 7 people refused to respond. Which of the following factors makes it least likely that a reliable conclusion can be drawn about the sports-watching preferences of all people in the town?
-
Solution
Survey research is an efficient way to estimate the preferences of a large population. In order to reliably generalize the results of survey research to a larger population, the participants should be randomly selected from all people in that population. Since this survey was conducted with a population that was not randomly selected, the results are not reliably representative of all people in the town. Therefore, of the given factors, where the survey was given makes it least likely that a reliable conclusion can be drawn about the sports-watching preferences of all people in the town.
Choice A is incorrect. In general, larger sample sizes are preferred over smaller sample sizes. However, a sample size of 117 people would have allowed a reliable conclusion about the population if the participants had been selected at random. Choice B is incorrect. Whether the population is large or small, a large enough sample taken from the population is reliably generalizable if the participants are selected at random from that population. Thus, a reliable conclusion could have been drawn about the population if the 117 survey participants had been selected at random. Choice C is incorrect. When giving a survey, participants are not forced to respond. Even though some people refused to respond, a reliable conclusion could have been drawn about the population if the participants had been selected at random.
On January 1, 2000, there were 175,000 tons of trash in a landfill that had a capacity of 325,000 tons. Each year since then, the amount of trash in the landfill increased by 7,500 tons. If y represents the time, in years, after January 1, 2000, which of the following inequalities describes the set of years where the landfill is at or above capacity?
-
Solution
Since there were 175,000 tons of trash in the landfill on January 1, 2000, and the amount of trash in the landfill increased by 7,500 tons each year after that date, the amount of trash, in tons, in the landfill y years after January 1, 2000 can be expressed as 175,000 + 7,500y. The landfill has a capacity of 325,000 tons. Therefore, the set of years where the amount of trash in the landfill is at (equal to) or above (greater than) capacity is described by the inequality 175,000 + 7,500y ≥ 325,000.
Choice A is incorrect. This inequality does not account for the 175,000 tons of trash in the landfill on January 1, 2000, nor does it accurately account for the 7,500 tons of trash that are added to the landfill each year after January 1, 2000. Choice B is incorrect. This inequality does not account for the 175,000 tons of trash in the landfill on January 1, 2000. Choice C is incorrect. This inequality represents the set of years where the amount of trash in the landfill is at or below capacity.
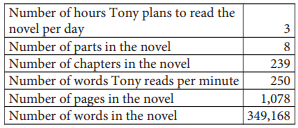
Tony is planning to read a novel. The table above shows information about the novel, Tony’s reading speed, and the amount of time he plans to spend reading the novel each day. If Tony reads at the rates given in the table, which of the following is closest to the number of days it would take Tony to read the entire novel?
-
Solution
Tony reads 250 words per minute, and he plans to read for 3 hours, which is 180 minutes, each day. Thus, Tony is planning to read 250 × 180 = 45,000 words of the novel per day. Since the novel has words, it will take Tony \(\frac{349,168}{45,000}\)≈ 7.76 days of reading to finish the novel.That is, it will take Tony 7 full days of reading and most of an 8th day of reading to finish the novel. Therefore, it will take Tony 8 days to finish the novel.
Choice A is incorrect and may result from an incorrect calculation or incorrectly using the numbers provided in the table. Choice C is incorrect and may result from taking the total number of words in the novel divided by the rate Tony reads per hour. Choice D is incorrect and may result from taking the total number of words in the novel divided by the number of pages in the novel.
A function f satisfies f(2) = 3 and f(3) = 5. A function g satisfies g(3) = 2 and g(5) = 6. What is the value of f(g(3)) ?
-
Solution
It is given that g(3) = 2. Therefore, to find the value of f(g(3)), substitute 2 for g(3): f(g(3)) = f(2) = 3.
Choices A, C, and D are incorrect and may result from misunderstandings about function notation.
A worker uses a forklift to move boxes that weigh either 40 pounds or 65 pounds each. Let x be the number of 40-pound boxes and y be the number of 65-pound boxes. The forklift can carry up to either 45 boxes or a weight of 2,400 pounds. Which of the following systems of inequalities represents this relationship?
-
Solution
Since x is the number of 40-pound boxes, 40x is the total weight, in pounds, of the 40-pound boxes; and since y is the number of 65-pound boxes, 65y is the total weight, in pounds, of the 65-pound boxes. The combined weight of the boxes is therefore 40x + 65y, and the total number of boxes is x + y. Since the forklift can carry up to 45 boxes or up to 2,400 pounds, the inequalities that represent these relationships are 40x + 65y ≤ 2,400 and x + y ≤ 45.
Choice B is incorrect. The second inequality correctly represents the maximum number of boxes on the forklift, but the first inequality divides, rather than multiplies, the number of boxes by their respective weights. Choice C is incorrect. The combined weight of the boxes, 40x + 65y, must be less than or equal to 2,400 pounds, not 45; the total number of boxes, x + y, must be less than or equal to 45, not 2,400. Choice D is incorrect. The second inequality correctly represents the maximum weight, in pounds, of the boxes on the forklift, but the total number of boxes, x + y, must be less than or equal to 45, not 2,400.
In a video game, each player starts the game with k points and loses 2 points each time a task is not completed. If a player who gains no additional points and fails to complete 100 tasks has a score of 200 points, what is the value of k ?
-
Solution
Since a player starts with k points and loses 2 points each time a task is not completed, the player’s score will be k − 2n after n tasks are not completed (and no additional points are gained). Since a player who fails to complete 100 tasks has a score of 200 points, the equation 200 = k − 100(2) must be true. This equation can be solved by adding 200 to each side, giving k = 400.
Choices A, B, and C are incorrect and may result from errors in setting up or solving the equation relating the player’s score to the number of tasks the player fails to complete. For example, choice A may result from subtracting 200 from the left-hand side of 200 = k − 100(2) and adding 200 to the right hand side.
y = x2 − 6x + 8
The equation above represents a parabola in the xy-plane. Which of the following equivalent forms of the equation displays the x-intercepts of the parabola as constants or coefficients?
-
Solution
The x-intercepts of the parabola represented by y = x2 − 6x + 8 in the xy-plane are the values of x for which y is equal to 0.The factored form of the equation, y = (x − 2)(x − 4), shows that y equals 0 if and only if x = 2 or x = 4. Thus, the factored form, y = (x − 2)(x − 4), displays the x-intercepts of the parabola as the constants 2 and 4.
Choices A, B, and C are incorrect because none of these forms shows the x-intercepts 2 and 4 as constants or coefficients.
When 4 times the number x is added to 12, the result is 8. What number results when 2 times x is added to 7 ?
-
Solution
When 4 times the number x is added to 12, the result is 12 + 4x. Since this result is equal to 8, the equation 12 + 4x = 8 must be true. Subtracting 12 from each side of 12 + 4x = 8 gives 4x = −4, and then dividing both sides of 4x = −4 by 4 gives x = −1. Therefore, 2 times x added to 7, or 7 + 2x, is equal to 7 + 2(−1) = 5.
Choice A is incorrect because −1 is the value of x, not the value of 7 + 2x.Choices C and D are incorrect and may result from calculation errors.
refer to the following information.
The amount of money a performer earns is directly proportional to the number of people attending the performance. The performer earns $120 at a performance where 8 people attend.
The performer uses 43% of the money earned to pay the costs involved in putting on each performance. The rest of the money earned is the performer’s profit. What is the profit the performer makes at a performance where 8 people attend?
-
Solution
If 43% of the money earned is used to pay for costs, then the rest, 57%, is profit. A performance where 8 people attend earns the performer $120, and 57% of $120 is $120 × 0.57 = $68.40.
Choice A is incorrect. The amount $51.60 is 43% of the money earned from a performance where 8 people attend, which is the cost of putting on the performance, not the profit from the performance. Choice B is incorrect. It is given that 57% of the money earned is profit, but 57% of $120 is not equal to $57.00. Choice D is incorrect. The profit can be found by subtracting 43% of $120 from $120, but 43% of $120 is $51.60, not $43.00. Thus, the profit is $120 − $51.60 = $68.40, not $120 − $43.00 = $77.00.
refer to the following information.
The amount of money a performer earns is directly proportional to the number of people attending the performance. The performer earns $120 at a performance where 8 people attend.
How much money will the performer earn when 20 people attend a performance?
-
Solution
The amount of money the performer earns is directly proportional to the number of people who attend the performance. Thus, by the definition of direct proportionality, M = kP, where M is the amount of money the performer earns, in dollars, P is the number of people who attend the performance, and k is a constant. Since the performer earns $120 when 8 people attend the performance, one can substitute 120 for M and 8 for P, giving 120 = 8k. Hence, k = 15, and the relationship between the number of people who attend the performance and the amount of money, in dollars, the performer earns is M = 15P. Therefore, when 20 people attend the performance, the performer earns 15(20) = 300 dollars.
Choices A, B, and D are incorrect and may result from either misconceptions about proportional relationships or computational errors.