In the xy-plane, the point (3, 6) lies on the graph of the function f(x) = 3x2 – bx + 12. What is the value of b ?
-
Solution
The correct answer is 11. It is given that the function f(x) passes through the point (3, 6). Thus, if x = 3, the value of f(x) is 6 (since the graph of f in the xy-plane is the set of all points (x, f(x)). Substituting 3 for x and 6 for f(x) in f(x) = 3x2 − bx + 12 gives 6 = 3(3)2 − b(3) + 12. Performing the operations on the right-hand side of this equation gives 6 = 3(9) − 3b + 12 = 27 − 3b + 12 = 39 −3b. Subtracting 39 from each side of 6 = 39 − 3b gives −33 = −3b, and then dividing each side of −3b = −33 by −3 gives the value of b as 11.
If h hours and 30 minutes is equal to 450 minutes, what is the value of h ?
-
Solution
The correct answer is 7. There are 60 minutes in each hour, and so there are 60h minutes in h hours. Since h hours and 30 minutes is equal to 450 minutes, it follows that 60h + 30 = 450. This equation can be simplified to 60h = 420, and so the value of h is \(\frac{420}{60}\) = 7.
A coastal geologist estimates that a certain country’s beaches are eroding at a rate of 1.5 feet per year. According to the geologist’s estimate, how long will it take, in years, for the country’s beaches to erode by 21 feet?
-
Solution
The correct answer is 14. Since the coastal geologist estimates that the country’s beaches are eroding at a rate of 1.5 feet every year, they will erode by 1.5x feet in x years. Thus, if the beaches erode by 21 feet in x years, the equation 1.5x = 21 must hold. The value of x is then \(\frac{21}{1.5}\) = 14. Therefore, according to the geologist’s estimate, it will take 14 years for the country’s beaches to erode by 21 feet.

The figure above shows a regular hexagon with sides of length a and a square with sides of length a. If the area of the hexagon is 384√3 square inches, what is the area, in square inches, of the square?
-
Solution
The regular hexagon can be divided into 6 equilateral triangles of side length a by drawing the six segments from the center of the regular hexagon to each of its 6 vertices. Since the area of the hexagon is 384√3 square inches, the area of each equilateral triangle will be \(\frac{384\sqrt{3}}{6}=64\sqrt{3}\) square inches.
Drawing any altitude of an equilateral triangle divides it into two 30°-60°-90° triangles. If the side length of the equilateral triangle is a, then the hypotenuse of each 30°-60°-90° triangle is a, and the altitude of the equilateral triangle will be the side opposite the 60° angle in each of the 30°-60°-90° triangles. Thus, the altitude of the equilateral triangle is √3⁄2a, and the area of the equilateral triangle is 1⁄2(a) (√3⁄2a) = √3⁄4a2. Since the area of each equilateral triangle is 64√3 square inches, it follows that a2 = 4⁄√3(64√3)= 256 square inches. And since the area of the square with side length a is a2,it follows that the square has area 256 square inches.
Choices B, C, and D are incorrect and may result from calculation or conceptual errors.
y = 3
y = ax2 + b
In the system of equations above, a and b are constants. For which of the following values of a and b does the system of equations have exactly two real solutions?
-
Solution
Substituting 3 for y in y = ax2 + b gives 3 = ax2 + b, which can be rewritten as 3 − b = ax2. Since y = 3 is one of the equations in the given system, any solution x of 3 − b = ax2 corresponds to the solution (x, 3)of the given system. Since the square of a real number is always nonnegative, and a positive number has two square roots, the equation 3 − b = ax2 will have two solutions for x if and only if (1) a > 0 and b < 3 or (2) a < 0 and b > 3. Of the values for a and b given in the choices, only a = −2, b = 4 satisfy one of these pairs of conditions.
Alternatively, if a = −2 and b = 4, then the second equation would be y = −2x2 + 4. The graph of this quadratic equation in the xy-plane is a parabola with y-intercept (0, 4) that opens downward. The graph of the first equation, y = 3, is the horizontal line that contains the point (0, 3). As shown below, these two graphs have two points of intersection, and therefore, this system of equations has exactly two real solutions. (Graphing shows that none of the other three choices produces a system with exactly two real solutions.)

Choices A, C, and D are incorrect and may result from calculation or conceptual errors.

In the xy-plane above, ABCD is a square and point E is the center of the square. The coordinates of points C and E are (7, 2) and (1, 0), respectively. Which of the following is an equation of the line that passes through points B and D ?
-
Solution
In the xy-plane, the slope m of the line that passes through the points (x1, y1) and (x2, y2) is m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\). Thus, the slope of the line through the points C(7, 2) and E(1, 0) is \(\frac{2 − 0}{7 − 1}\), which simplifies to 2⁄6 = 1⁄3. Therefore, diagonal AC has a slope of 1⁄3. The other diagonal of the square is a segment of the line that passes through points B and D. The diagonals of a square are perpendicular, and so the product of the slopes of the diagonals is equal to −1. Thus, the slope of the line that passes through B and D is −3 because 1⁄3(−3) = −1. Hence, an equation of the line that passes through B and D can be written as y = −3x + b, where b is the y-intercept of the line. Since diagonal BD will pass through the center of the square, E(1, 0), the equation 0 = −3(1) + b holds. Solving this equation for b gives b = 3. Therefore, an equation of the line that passes through points B and D is y = −3x + 3, which can be rewritten as y = −3(x − 1).
Choices A, C, and D are incorrect and may result from a conceptual error or a calculation error.

Two samples of water of equal mass are heated to 60 degrees Celsius (°C). One sample is poured into an insulated container, and the other sample is poured into a non-insulated container. The samples are then left for 70 minutes to cool in a room having a temperature of 25°C. The graph above shows the temperature of each sample at 10-minute intervals. Which of the following statements correctly compares the average rates at which the temperatures of the two samples change?
-
Solution
According to the graph, in the interval from 0 to 10 minutes, the non-insulated sample decreased in temperature by about 18°C, while the insulated sample decreased by about 8°C; in the interval from 10 to 20 minutes, the non-insulated sample decreased in temperature by about 9°C, while the insulated sample decreased by about 5°C; in the interval from 40 to 50 minutes, the non-insulated sample decreased in temperature by about 1°C, while the insulated sample decreased by about 3°C; and in the interval from 50 to 60 minutes, the non-insulated sample decreased in temperature by about 1°C, while the insulated sample decreased by about 2°C. The description in choice D accurately summarizes these rates of temperature change over the given intervals. (Note that since the two samples of water have equal mass and so must lose the same amount of heat to cool from 60°C to 25°C, the faster cooling of the non-insulated sample at the start of the cooling process must be balanced out by faster cooling of the insulated sample at the end of the cooling process.)
Choices A, B, and C are incorrect. None of these descriptions accurately compares the rates of temperature change shown in the graph for the 10-minute intervals.
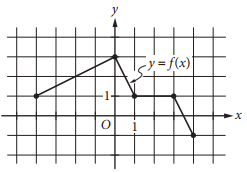
The complete graph of the function f is shown in the xy-plane above. Which of the following are equal to 1 ?
I. f(−4)
II. f(3⁄2)
III. f(3)
-
Solution
The definition of the graph of a function f in the xy-plane is the set of all points (x, f(x)). Thus, for −4 ≤ a ≤ 4, the value of f(a) is 1 if and only if the unique point on the graph of f with x-coordinate a has y-coordinate equal to 1. The points on the graph of f with x-coordinates −4,3⁄2, and 3 are, respectively, (−4, 1),(3⁄2, 1), and (3, 1). Therefore, all of the values of f given in I, II, and III are equal to 1.
Choices A, B, and C are incorrect because they each omit at least one value of x for which f(x) = 1.
The graph of the linear function f has intercepts at (a , 0) and (0, b) in the xy-plane. If a + b = 0 and a ≠ b, which of the following is true about the slope of the graph of f ?
-
Solution
In the xy-plane, the slope m of the line that passes through the points (x1, y1) and (x2, y2) is given by the formula m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\). Thus, if the graph of the linear function f has intercepts at (a, 0) and (0, b), then the slope of the line that is the graph of y = f(x) is m = \(\frac{0 − b}{a − 0}=-\frac{b}{a}\). It is given that a + b = 0, and so a = −b. Finally, substituting −b for a in m = b⁄a gives m = −b⁄−b= 1, which is positive.
Choices B, C, and D are incorrect and may result from a conceptual misunderstanding or a calculation error.
x2 + y2 + 4x − 2y = −1
The equation of a circle in the xy-plane is shown above. What is the radius of the circle?
-
Solution
The equation of a circle with center (h, k) and radius r is (x − h)2 + (y − k)2 = r2. To put the equation x2 + y2 + 4x − 2y = −1 in this form, complete the square as follows:
x2 + y2 + 4x − 2y = −1
(x2 + 4x) + (y2 − 2y) = −1
(x2 + 4x + 4) −4 + (y2 − 2y + 1) − 1 = −1
(x + 2)2 + (y − 1)2 − 4 − 1 = −1
(x + 2)2 + (y − 1)2 = 4 = 22
Therefore, the radius of the circle is 2.
Choice C is incorrect because it is the square of the radius, not the radius. Choices B and D are incorrect and may result from errors in rewriting the given equation in standard form.
