h = − 4.9t2 + 25t
The equation above expresses the approximate height h, in meters, of a ball t seconds after it is launched vertically upward from the ground with an initial velocity of 25 meters per second. After approximately how many seconds will the ball hit the ground?
-
Solution
When the ball hits the ground, its height is 0 meters. Substituting 0 for h in h = −4.9t2 + 25t gives 0 = −4.9t2 + 25t, which can be rewritten as 0 = t(−4.9t + 25). Thus, the possible values of t are t = 0 and t =\(\frac{25}{4.9}\) ≈ 5.1. The time t = 0 seconds corresponds to the time the ball is launched from the ground, and the time t ≈ 5.1 seconds corresponds to the time after launch that the ball hits the ground. Of the given choices, 5.0 seconds is closest to 5.1 seconds, so the ball returns to the ground approximately 5.0 seconds after it is launched.
Choice A, B, and C are incorrect and could arise from conceptual or computation errors while solving 0 = −4.9t2 + 25t for t.
Which of the following is an equation of a circle in the xy-plane with center (0, 4) and a radius with endpoint (4⁄3,5)?
-
Solution
The equation of a circle can be written as (x − h)2 + (y − k)2 = r2 where (h, k) are the coordinates of the center of the circle and r is the radius of the circle. Since the coordinates of the center of the circle are (0, 4), the equation is x2 + (y − 4)2 = r2, where r is the radius. The radius of the circle is the distance from the center, (0, 4), to the given endpoint of a radius, (4⁄3, 5). By the distance formula, r2 = (4⁄3 − 0)4⁄3 + (5 − 4)4⁄3 = \(\frac{25}{9}\). Therefore, an equation of the given circle is x2 + (y − 4)2 = \(\frac{25}{9}\) .
Choice B is incorrect; it results from the incorrect equation (x + h)2 + (y + k)2 = r2. Choice C is incorrect; it results from using r instead of r2 in the equation for the circle. Choice D is incorrect; it results from using the incorrect equation (x + h)2 + (y + k)2 = 1⁄r.
refer to the following information.
Annual Budgets for Different Programs in Kansas, 2007 to 2010

The table above lists the annual budget, in thousands of dollars, for each of six different state programs in Kansas from 2007 to 2010.
Of the following, which program’s ratio of its 2007 budget to its 2010 budget is closest to the human resources program’s ratio of its 2007 budget to its 2010 budget?
-
Solution
The human resources budget in 2007 was 4,051,050 thousand dollars, and the human resources budget in 2010 was 5,921,379 thousand dollars. Therefore, the ratio of the 2007 budget to the 2010 budget is slightly greater than4⁄6 =2⁄6. Similar estimates for agriculture/natural resources give a ratio of the 2007 budget to the 2010 budget of slightly greater than3⁄4 ; for education, a ratio of slightly greater than 2⁄3 ; for highways and transportation, a ratio of slightly less than 5⁄6; and for public safety, a ratio of slightly greater than 5⁄9.Therefore, of the given choices, education’s ratio of the 2007 budget to the 2010 budget is closest to that of human resources.
Choices A, C, and D are incorrect because the 2007 budget to 2010 budget ratio for each of these programs in these choices is further from the corresponding ratio for human resources than the ratio for education.
refer to the following information.
Annual Budgets for Different Programs in Kansas, 2007 to 2010

The table above lists the annual budget, in thousands of dollars, for each of six different state programs in Kansas from 2007 to 2010.
Which of the following best approximates the average rate of change in the annual budget for agriculture/natural resources in Kansas from 2008 to 2010 ?
-
Solution
The average rate of change in the annual budget for agriculture/natural resources from 2008 to 2010 is the total change from to 2008 to 2010 divided by the number of years, which is 2. The total change in the annual budget for agriculture/natural resources from 2008 to 2010 is 488,106 − 358,708 = 129,398, in thousands of dollars, so the average change in the annual budget for agriculture/natural resources from 2008 to 2010 is \(\frac{\$ 129,398,000}{2}\) = $64,699,000 per year. Of the options given, this average rate of change is closest to $65,000,000 per year.
Choices A and C are incorrect; they could result from errors in setting up or calculating the average rate of change. Choice D is incorrect; $130,000,000 is the approximate total change from 2008 to 2010, not the average change from 2008 to 2010.
Dreams Recalled during One Week
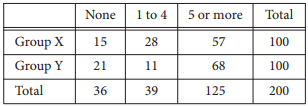
The data in the table above were produced by a sleep researcher studying the number of dreams people recall when asked to record their dreams for one week. Group X consisted of 100 people who observed early bedtimes, and Group Y consisted of 100 people who observed later bedtimes. If a person is chosen at random from those who recalled at least 1 dream, what is the probability that the person belonged to Group Y ?
-
Solution
The probability that a person from Group Y who recalled at least 1 dream was chosen from the group of all people who recalled at least 1 dream is equal to the number of people in Group Y who recalled at least 1 dream divided by the total number of people in the two groups who recalled at least 1 dream. The number of people in Group Y who recalled at least 1 dream is the sum of the 11 people in Group Y who recalled 1 to 4 dreams and the 68 people in Group Y who recalled 5 or more dreams: 11 + 68 = 79. The total number of people who recalled at least 1 dream is the sum of the 79 people in Group Y who recalled at least 1 dream, the 28 people in Group X who recalled 1 to 4 dreams, and the 57 people in Group X who recalled 5 or more dreams: 79 + 28 + 57 = 164. Therefore, the probability is \(\frac{79}{164}\).
Choice A is incorrect; it is the number of people in Group Y who recalled 5 or more dreams divided by the total number of people in Group Y. Choice B is incorrect; it uses the total number of people in Group Y as the denominator of the probability. Choice D is incorrect; it is the total number of people in the two groups who recalled at least 1 dream divided by the total number of people in the two groups.
Alma bought a laptop computer at a store that gave a 20 percent discount off its original price. The total amount she paid to the cashier was p dollars, including an 8 percent sales tax on the discounted price. Which of the following represents the original price of the computer in terms of p ?
-
Solution
Let x be the original price of the computer, in dollars. The discounted price is 20 percent off the original price, so x − 0.2x = 0.8x is the discounted price, in dollars. The tax is 8 percent of the discounted price, so 0.08(0.8x) is the tax on the purchase, in dollars. The price p, in dollars, that Alma paid the cashiers is the sum of the discounted price and the tax: p = 0.8x + (0.08)(0.8x) which can be rewritten as p = 1.08(0.8x). Therefore, the original price, x, of the computer, in dollars, can be written as \(\frac{p}{(0.8)(1.08)}\) in terms of p.
Choices A, B, and C are incorrect; each choice either switches the roles of the original price and the amount Alma paid, or incorrectly combines the results of the discount and the tax as 0.8 + 0.08 = 0.88 instead of as (0.8)(1.08).
A food truck sells salads for $6.50 each and drinks for $2.00 each. The food truck’s revenue from selling a total of 209 salads and drinks in one day was $836.50. How many salads were sold that day?
-
Solution
To determine the number of salads sold, write and solve a system of two equations. Let x equal the number of salads sold and let y equal the number of drinks sold. Since the number of salads plus the number of drinks sold equals 209, the equation x + y = 209 must hold. Since each salad cost $6.50, each soda cost $2.00, and the total revenue was $836.50, the equation 6.50x + 2.00y = 836.50 must also hold. The equation x + y = 209 is equivalent to 2x + 2y = 418, and subtracting each side of 2x + 2y = 418 from the respective side of 6.50x + 2.00y = 836.50 gives 4.5x = 418.50. Therefore, the number of salads sold, x, was x = \(\frac{418.50}{4.50}\) = 93.
Choices A, C, and D are incorrect and could result from errors in writing the equations and solving the system of equations. For example, choice C could have been obtained by dividing the total revenue, $836.50, by the total price of a salad and a soda, $8.50, and then rounding up.
y < -x + a y > x + b
In the xy-plane, if (0, 0) is a solution to the system of inequalities above, which of the following relationships between a and b must be true?
-
Solution
Since (0, 0) is a solution to the system of inequalities, substituting 0 for x and 0 for y in the given system must result in two true inequalities. After this substitution, y < −x + a becomes 0 < a, and y > x + b becomes 0 > b. Hence, a is positive and b is negative. Therefore, a > b.
Choice B is incorrect because b > a cannot be true if b is negative and a is positive. Choice C is incorrect because it is possible to find an example where (0, 0) is a solution to the system, but |a| < |b|; for example, if a = 6 and b = −7. Choice D is incorrect because the equation a = −b could be true, but doesn’t have to be true; for example, if a = 1 and b = −2.

The complete graph of the function f is shown in the xy-plane above. For what value of x is the value of f(x) at its minimum?
-
Solution
The minimum value of the function corresponds to the y-coordinate of the point on the graph that is the lowest along the vertical or y-axis. Since the grid lines are spaced 1 unit apart on each axis, the lowest point along the y-axis has coordinates (−3, −2). Therefore, the value of x at the minimum of f(x) is −3.
Choice A is incorrect; −5 is the smallest value for an x-coordinate of a point on the graph of f, not the lowest point on the graph of f. Choice C is incorrect; it is the minimum value of f, not the value of x that corresponds to the minimum of f. Choice D is incorrect; it is the value of x at the maximum value of f, not at the minimum value of f
refer to the following information.

The graph above displays the total cost C, in dollars, of renting a boat for h hours.4
Which of the following represents the relationship between h and C ?
-
Solution
The relationship between h and C is represented by any equation of the given line. The C-intercept of the line is 5. Since the points (0, 5) and (1, 8) lie on the line, the slope of the line is \(\frac{8 − 5}{1 − 0}=\frac{3}{1}=3\). Therefore,the relationship between h and C can be represented by C = 3h + 5, the slope-intercept equation of the line.
Choices A and D are incorrect because each uses the wrong values for both the slope and intercept. Choice B is incorrect; this choice would result from computing the slope by counting the number of grid lines instead of using the values represented by the axes.