A group of 24 students was polled as to whether they enjoy biology class, chemistry class, both, or neither. The results are shown in the table below:
| Biology | Chemistry | |
| Enjoy | 14 | 18 |
| Don’t Enjoy | 10 | 6 |
Given the above data, which of the following conclusions is true?
-
Solution
The best way to approach this question is through POE.
According to the data in the table, the ratio of those who enjoy biology to those who enjoy chemistry is 14 to 18, which can be reduced to a ratio of 7 to 9; eliminate (A).
The ratio of those who enjoy chemistry to those who don't enjoy chemistry is 18 to 6, which can be reduced to a ratio of 3 to 1; eliminate (B).
The ratio of those who enjoy biology to those who don't enjoy chemistry is 14 to 6, which can be reduced to a ratio of 7 to 3; eliminate (C).
The ratio of those who don't enjoy biology to those who enjoy chemistry is 10 to 18, which can be reduced to a ratio of 5 to 9; this matches (D).
Rob has his favorite guitar tuned up and ready to bring to a performance by his cover band at a local venue Saturday. He decides at the last minute to bring x additional guitars, just in case his favorite guitar has an issue. If the total number of guitars that Robert brings to the performance can be modeled as x + 1, what does the “+ 1” account for in the expression?
-
Solution
Since the question states that Rob is planning to bring his favorite guitar plus x additional guitars, he will have a total of x + 1 guitars.
The question states that the variable x represents the number of additional guitars, so the number 1 must represent Rob's favorite guitar, which is (B).
Merry joined an online community that charges a monthly fee of $15. A one-time enrollment fee of $50 was charged when she joined. Which of the following represents the total amount of fees that Merry has paid to the community organizers after m months, in dollars?
-
Solution
Whenever the question includes variables, plug in.
If m = 2, then Merry would pay the one-time enrollment fee plus 2 months' worth of monthly fees, which is 50 + 15(2) = 80.
Plug in 2 for m in the answer choices to see which answer equals the target number of 80.
In (A), 15(2) + 50 = 80. This is the target number, so leave this answer, but be sure to check the other choices just in case.
In (B), 15 + 50(2) = 115. In (C), 15(2) - 50 = -20, and in (D), (15 + 50)(2) = 130.
Since none of the other answer choices equals the target number, the correct answer is (A).
If 3y = y + 2, what is the value of 2y ?
-
Solution
To solve this question, simply subtract y from both sides of the equation to get 2y = 2, which is (B).
The flu shot for a flu season is created from four strains of the flu virus, named Strain A, B, C, and D, respectively. Medical researchers use the following data to determine the effectiveness of the vaccine over the flu season. Table 1 shows the effectiveness of the vaccine against each of these strains individually. The graph below the table shows the prevalence of each of these strains during each month of the flu season, represented as a percentage of the overall cases of flu that month.
Table 1
Strain Effectiveness
A 35%
B 13%
C 76%
D 68%
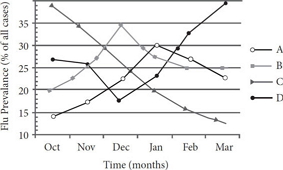
For the strain against which the flu shot was the most effective, approximately how effective was the shot overall when that strain was least prevalent?
-
Solution
The flu shot is most effective against Strain C, which is least prevalent in March.
To determine the overall efficacy of the flu shot at this time, multiply the prevalence of each strain of flu by the efficacy of the flu shot against that strain, and then add those products to get a weighted average of the efficacy of the shot: (0.23 × 0.35) + (0.25 × 0.13) + (0.13 × 0.76) + (0.39 × 0.68) = 0.477 = 47.7%, which is closest to (D).
The function g is defined by g(x) = 2x2 – dx – 6, where d is a constant. If one of the zeros of g is 6, what is the value of the other zero of g ?
-
Solution
The zero of g is the value of the variable, in this case x, when the equation is set to 0.
This is also called the root or solution of an equation.
Set the equation to 0 to get 0 = 2x2 - dx - 6.
Plug 6 in for x to get 0 = 2(62) - d(6) - 6.
Simplify the equation to get 0 = 72 - 6d - 6, or 0 = 66 - 6d.
Solve for d to get -66 = -6d, so 11 = d.
Plug 11 in for d and set the quadratic to 0 to get 0 = 2x2 - 11x - 6.
Factor the equation to get 0 = (x - 6)(2x + 1).
The other zero of the equation is when 2x + 1 = 0.
Solve for x to get 2x = -1, or x = -1⁄2.
The correct answer is (C).
If (i413)(ix) = 1, then what is one possible value of x ?
-
Solution
ia = 1 when a is a multiple of 4.
Using your exponents rules, 413 + x must also be a multiple of 4.
Plug in the answers and look for what makes 413 + x a multiple of 4.
Only (D) works.
Students in a physics class are studying how the angle at which a projectile is launched on level ground affects the projectile’s hang time and horizontal range. Hang time can be calculated using the formula t = \(\frac{2v\cdot sin\left ( \Theta \right )}{g}\), where t is the hang time in seconds, v is the initial launch velocity, θ is the projectile angle with respect to level ground, and g is the acceleration due to gravity, defined as 9.8 m/s2. Horizontal range can be calculated using the formula R = \(\frac{v^{2} \cdot sin\left ( 2\Theta \right )}{g}\), where R is the distance the projectile travels from the launch site, in feet. Which of the following gives the value of v, in terms of R, t, and θ ?
-
Solution
Whenever there are variables in the question and in the answers, think Plugging In.
The question states the value of g, but it is a constant and a weird one at that.
Pick numbers for all the variables that will make the math more straightforward.
If v = 4 and g = 2, then \(t = \frac{2\left (4 \right )\cdot sin \left (\theta \right )}{2} = \frac{8\cdot sin \left (\theta \right )}{2} = 4 \cdot sin \left (\theta \right )\) and \(R = \frac{\left (4 \right )^{2} \cdot sin \left (2\theta \right )}{2} = \frac{16 \cdot sin \left (2\theta \right )}{2} = 8 \cdot sin \left (2\theta \right )\).
Plug these values into the answers to see which equation works.
Choice (A) becomes \(4 = \frac{4 \cdot sin\left ( \theta \right ) \cdot sin\left ( \theta \right )}{2\left [ 8 sin\left ( 2\theta \right )sin\left ( \theta \right )\right ]}\).
Simplify the right side of the equation to get \(4 = \frac{4 \cdot sin\left ( \theta \right ) \cdot sin\left ( \theta \right )}{16 sin\left ( 2\theta \right )sin\left ( \theta \right )}\), or \(4 = \frac{sin\left ( \theta \right )}{4sin\left ( 2\theta \right )}\).
This will not simplify further, so eliminate (A).
Choice (B) becomes \(4 = \frac{2 \left [4 sin\left ( \theta \right ) \right ] sin\left ( \theta \right )}{8 sin\left ( 2\theta \right )sin\left ( \theta \right )}\).
Simplify the right side of the equation to get \(4 = \frac{8 sin\left ( \theta \right ) sin\left ( \theta \right )}{8 sin\left ( 2\theta \right )sin\left ( \theta \right )}\) or \(4 = \frac{sin\left ( \theta \right )}{sin\left ( 2\theta \right )}\).
Eliminate (B).
Choice (C) becomes \(4 = \frac{2 \left [8 sin\left ( 2\theta \right ) \right ] sin\left ( \theta \right )}{\left (4 sin\left ( 2\theta \right ) \right )\left (sin\left ( 2\theta \right ) \right )}\).
Distribute the 2 to get \(4 = \frac{16 sin\left ( 2\theta \right ) sin\left ( \theta \right )}{\left (4 sin\left ( \theta \right ) \right )\left (sin\left ( 2\theta \right ) \right )}\).
Reduce the equation to get or 4 = 16⁄4 or 4 = 4.
The correct answer is (C).
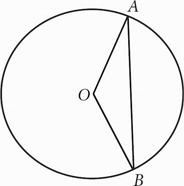
If the radius of the circle above is x, ∠AOB = 120°, and O is the center of the circle, what is the length of chord AB in terms of x ?
-
Solution
You can start by Plugging In a value for x; try x = 4.
Because angle AOB is 120° and the triangle is isosceles, angles A and B are each 30°.
Cut triangle AOB in half to make two 30-60-90 triangles with a hypotenuse of 4 and sides of 2 and 2√3.
The side with length 2√3 lies on chord AB.
Double it to get the total length: 4√3 or just √3x, which is (B) when you put x = 4 into the answer choices.
Melanie puts $1,100 in an investment account that she expects will make 5% interest for each three-month period. However, after a year she realizes she was wrong about the interest rate and she has $50 less than she expected. Assuming the interest rate the account earns is constant, which of the following equations expresses the total amount of money, x, she will have after t years using the actual rate?
-
Solution
The formula for compound interest is A = P(1 + r)t, where P is the starting principle, r is the rate expressed as a decimal, and t is the number of times the interest is compounded.
Melanie received less than 5% interest, so you can eliminate (B) because 1.05 = 1 + 0.05, indicating she was receiving 5% interest.
You can also eliminate (C) because over the course of a year the interest is compounded 4 times, not 1⁄3 of a time.
Because Melanie invested $1,100 at what she thought was 5% compounded 4 times (12 months in a year ÷ 3 months per period), she expected 1,100(1 + 0.05)4 = $1,337.06 after a year.
Instead, she has 1,337.06 - 50 = $1,287.06 after one year.
Because t is in years in the answer choices, make t = 1 in (A) and (D) and eliminate any choice which does not equal 1,287.06.
Only (A) works.