The value of 7x2 + 3 is how much more than the value of 7x2 – 9?
-
Solution
Don't forget to distribute the negative when simplifying the difference:
(7x2 + 3) - (7x2 - 9) = 7x2 + 3 - 7x2 + 9 = 12
Which of the following expressions is equivalent to \(\sqrt{16x^{9}y^{6}}\)?
-
Solution
\(\sqrt{16x^{9}y^{6}}\)
= \(\sqrt{\left (4 \right )^{2} \times \left (x^{4} \right )^{2} \times x \times \left (y^{3} \right )^{2}}\)
= 4x4y3 √x
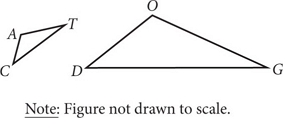
If ΔCAT shown above is similar to ΔDOG, and the ratio of the length of \(\overline{TC} \; to \; \overline{GD}\) is 2:7, which of the following ratios must also be equal to 2:7?
-
Solution
You can eliminate B immediately because corresponding angles of similar triangles are congruent, so they are always in a 1:1 ratio.
You can also eliminate A because side CA does not correspond to side DG (CA corresponds to DO), so you cannot say that they will be in the same ratio.
Because the side lengths are proportional, when you add the lengths of all the side lengths (the perimeter), this number will be in the same proportion, so (D) is correct.
You can check this by assigning numbers that are in the ratio 2:7 and finding the perimeter of each triangle:
TC = 2 and GD = 7
CA = 4 and DO = 14
AT = 6 and OG = 21
Perimeter of triangle CAT = 2 + 4 + 6 = 12
Perimeter of triangle DOG = 7 + 14 + 21 = 42
12 : 42 = 2 : 7
A hospital hosts an annual charity drive in which volunteers sell first aid kits to raise money for the pediatric ward. The hospital ordered too many kits last year, so it already has some to start this year’s drive with. The project manager estimates, based on last year’s sales, that the hospital needs to order an additional 50 boxes of kits. The function k(b) = 12b + 32, where b is the number of boxes ordered, represents the number of kits the hospital will have after the order arrives. When the project manager places the order, she is told that the company has changed the number of kits per box to 8. How many more boxes will she need to order to end up with the same number of kits that she had originally planned for?
-
Solution
The function represents the number of kits the hospital will have, so k(b) is the total number of kits.
The question tells you that b is the number of boxes ordered, which you also know to be 50.
Because b is multiplied by 12, this must be the number of kits per box.
Finally, 32 is simply added to the equation, which must mean it represents the kits left over from last year's charity drive.
Now, look at the question. It states that the company has changed the number of kits per box to 8.
Evaluate the original function at b = 50 to see how many kits the hospital would have had: k(50) = 12(50) + 32 = 632.
Now, substitute this for k(b) in the new function, replacing the 12 with the 8, and solve for b:
632 = 8b + 32
600 = 8b
75 = b
Be careful-this is not the answer. She needs to order 75 - 50 = 25 more boxes than she would have had to order at 12 kits per box.
In a certain board game, where playing involves a specific number of cards and a specific number of players, three cards are removed from the deck and kept in an envelope, while the rest of the cards are distributed equally among the players. The scenario can be represented by the equation given above. What does the variable c represent in this scenario?
-
Solution
In the scenario, there are a specified number of cards in the deck, from which 3 are removed, or subtracted.
This means b must represent the initial number of cards in the deck, from which the remaining cards (b - 3) are distributed, or divided, equally among the players.
This means c must represent the number of players among whom the cards are divided, making (A) correct.
Although it is not asked for in the question, the result of performing all the operations (a) represents the number of cards each player receives.
If g is a function defined over the set of all real numbers and g(x – 1) = 3x2 + 5x – 7, then which of the following defines g(x)?
-
Solution
To keep things organized, let u = x - 1, the old input.
This means x = u + 1. Substitute this into g and simplify:
g(u) = 3(u + 1)2 + 5(u + 1) - 7
= 3(u2 + 2u + 1) + 5u + 5 - 7
= 3u2 + 6u + 3 + 5u + 5 - 7
= 3u2 + 11u + 1
This means g(u) = 3u2 + 11u + 1.
When working with function notation, you evaluate the function by substituting a given input value for the variable in the parentheses.
Here, if the input value is x, then g(x) = 3x2 + 11x + 1.
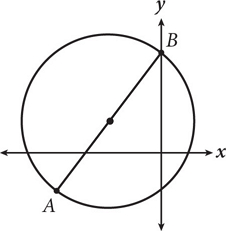
The circle shown is given by the equation x2 + y2 + 6x – 4y = 12. What is the shortest distance from A to B?
-
Solution
The shortest distance from A to B is through the center of the circle, along the diameter, which is twice the radius, so you need to find r.
To do this, complete the square for the x-terms and for the y-terms.
Start by reordering the terms.
Then, take the coefficient of the x-term and divide it by 2, square it, and add the result to the two terms with x-variables.
Do the same with the y-term. Remember, you must also add these amounts to the other side of the equation.
This creates a perfect square of x-terms and y-terms, and the equation will look more like a circle.
x2 + y2 + 6x - 4y = 12
x2 + 6x + y2 - 4y = 12
(x2 + 6x + 9) + (y2 - 4y + 4) = 12 + 9 + 4
(x + 3)2 + (y - 2)2 = 25
This means that the radius of the circle is √25 = 5 so the diameter is 10, which is also the distance from A to B.
Note that you can do a quick check of your work by looking at the center; according to the equation, the center is (-3, 2), which appears to match the location of the center on the graph.
⇒ \(\frac{4x}{x – 7} + \frac{2x}{2x – 14} = \frac{70}{2\left ( x – 7 \right )}\)
What value(s) of x satisfy the equation above?
-
Solution
The denominators are almost the same already; you just need to multiply the top and bottom of the first term by 2, factor the denominator of the second term, and you'll be ready to solve the equation.
\(\frac{2}{2}\left (\frac{4x}{x - 7} \right ) + \frac{2x}{2x - 14} = \frac{70}{2\left ( x - 7 \right )}\)
\(\frac{8x}{2\left (x - 7 \right )} + \frac{2x}{2\left (x - 7 \right )} = \frac{70}{2\left ( x - 7 \right )}\)
Now that the denominators are all the same, you can solve the equation represented by the numerators.
8x + 2x = 70
10x = 70
x = 7
Be careful-this isn't the correct answer.
Because there are variables in the denominator, you must check the solution to make sure it isn't extraneous, or in other words, doesn't cause a 0 in the denominator of any term.
Unfortunately, if x = 7, then all of the denominators are zero (and division by zero is not possible), so the equation has no solution.
⇒ \(\left\{\begin{matrix} y & – & \frac{2}{k}x & \leq & 0 \\ \frac{1}{k}x & – & \frac{1}{2}y & \leq -1 & \end{matrix}\right.\)
If the system of inequalities shown has no solution, what is the value of k?
-
Solution
Start by writing each equation in slope-intercept form to help you envision what the graphs will look like.
You'll need to multiply the second equation by -2, so don't forget to flip the inequality symbol.
\(y - \frac{2}{k}x \leq 0 \rightarrow y \leq \frac{2}{k}x\)
\(\frac{1}{k}x - \frac{1}{2}y \leq -1 \rightarrow -\frac{1}{2}y \leq -\frac{1}{k}x - 1\) → \(y \geq \frac{2}{k}x + 2\)
Now, think about the graphs.
The first equation has a slope of 2⁄k, a y-intercept of 0, and is shaded below the line.
The second equation also has a slope of 2⁄k, but it has a y-intercept of 2 and is shaded above the line.
This means that no matter what value of k is used (other than 0), the two lines are parallel and shaded in opposite directions, and thus there are infinitely many values of k that produce a system with no solution.
If 0 < 1 – a⁄3 ≤ 1⁄2, which of the following is not a possible value of a?
-
Solution
You don't need to separate this compound inequality into pieces.
Just remember, whatever you do to one piece, you must do to all three pieces.
Don't forget to flip the inequality symbols if you multiply or divide by a negative number.
0 < 1 - a⁄3 ≤ 1⁄2
6(0) < 6(1 - a⁄3) ≤ 6(1⁄2)
0 < 6 - 2a ≤ 3
-6 < -2a ≤ -3
3 > a ≥ 3⁄2
1.5 ≤ a < 3
Now, read the inequality symbols carefully.
The value of a is between 1.5 and 3, including 1.5, but not including 3, so (D) is the correct answer.